Monodromy literally means "once around." The term is applied in mathematics to systems that run around a singularity. In these systems, a parameter that describes the state of the system changes when the system loops around the singularity. Since monodromy’s discovery in 1980, mathematicians have predicted that many physical systems have it, including pendulums and tops as well as atoms and molecules.
Fellow Heather Lewandowski’s group recently decided to do an experiment to see whether a pendulum on a spring does, in fact, have monodromy as predicted in 2004. "Even though the theory of monodromy has been around for almost 30 years, nobody had actually tested the classical prediction in the lab before," she said. Lewandowski was assisted by graduate students Noah Fitch and Paul Parazzoli, undergraduate student Carrie Weidner, and visiting mathematician H. R. Dullin (University of Sydney).
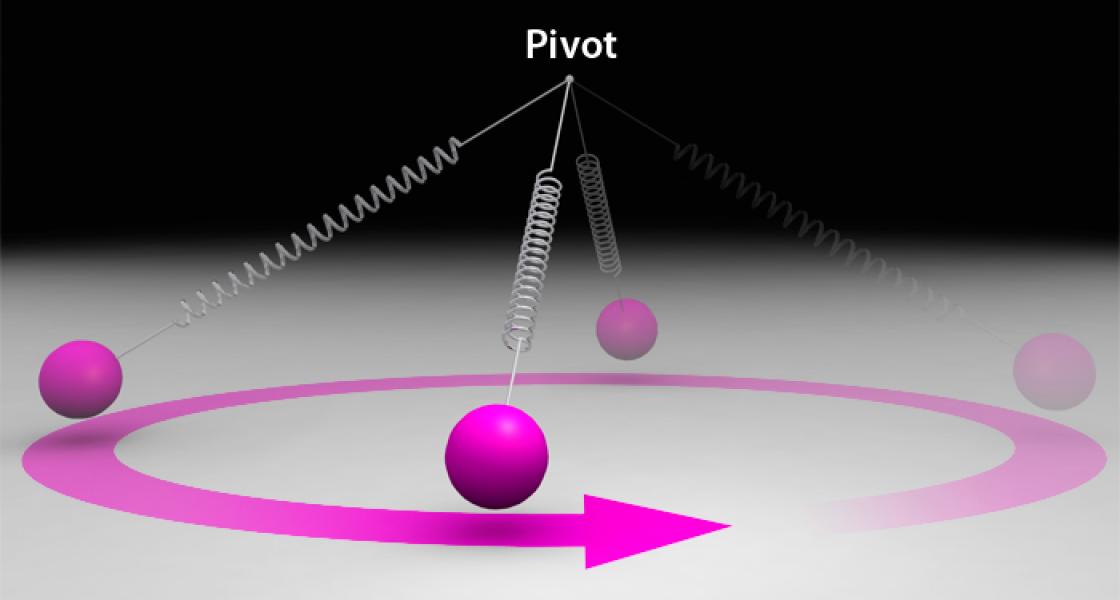
The researchers focused on the behavior of the pendulum on a spring when the swinging and bouncing frequencies were in a ratio of 1:2. This frequency ratio facilitated energy transfer between the swinging and bouncing modes and resulted in the evolution of pure bouncing into pure swinging, then back into pure bouncing — over and over again until damping stopped the cycle. The ellipses traced by the swinging pendulum precessed at a constant step angle between successive swinging episodes.
To see whether this system had monodromy, Lewandowski’s group performed two sets of experiments. Each one had a different set of initial conditions corresponding to different initial positions of the pendulum bob. These sets of initial conditions formed two loops. One loop enclosed a singularity, and the other did not. The researchers measured the step angles at the beginning and at the end of the loops. They found the net change was zero only for the loop that did not enclose the singularity. The observation that the change in the step angle of the singularity-enclosing loop was not zero was experimental proof that monodromy existed in this system.
In this simple classical system, monodromy was easily detected. Consequently, the group’s experiments can now provide a foundation for a deeper understanding of quantum mechanical monodromy. Quantum mechanical monodromy can profoundly influence the energy spectra of atoms and molecules. It also plays a role in molecular rearrangements and the behavior of polar molecules in electric fields (where molecules swing back and forth like pendulums).
For instance, the classical monodromy confirmed in the pendulum-on-a-spring experiment is analogous to the bending and stretching behavior of a CO2 molecule — if CO2 is viewed as three balls attached by two springs. The stretching modes (bouncing) of the two C–O bonds are in a 2:1 resonance with the bending mode (swinging) of the molecule. The coupling between the stretching and bending modes of CO2 is analogous to the resonant coupling between bouncing and swinging in the pendulum-on-a-spring system.
Molecules like CO2 are one reason why Lewandowski decided to explore classical monodromy in the first place. Her research focuses on collisions of simple cold molecules, and she’s already built the sort of system that could one day be used to probe quantum mechanical monodromy. - Julie Phillips