Quantum sensors help physicists understand the world better by measuring time passage, gravity fluctuations, and other effects at the tiniest scales. For example, one quantum sensor, the LIGO gravitational wave detector, uses quantum entanglement (or the interdependence of quantum states between particles) within a laser beam to detect distance changes in gravitational waves up to one thousand times smaller than the width of a proton!
LIGO isn’t the only quantum sensor harnessing the power of quantum entanglement. This is because entangled particles are generally more sensitive to specific parameters, giving more accurate measurements.
While researchers can generate entanglement between particles, the entanglement may only be useful sometimes for sensing something of interest. To measure the “usefulness” of quantum entanglement for quantum sensing, physicists calculate a mathematical value, known as the Quantum Fisher Information (QFI), for their system. However, physicists have found that the more quantum states in the system, the harder it becomes to determine which QFI to calculate for each state.
To overcome this challenge, JILA Fellow Murray Holland and his research team proposed an algorithm that uses the Quantum Fisher Information Matrix (QFIM), a set of mathematical values that can determine the usefulness of entangled states in a complicated system.
Their results, published in Physical Review Letters as an Editor’s Suggestion, could offer significant benefits in developing the next generation of quantum sensors by acting as a type of “shortcut” to find the best measurements without needing a complicated model.
“Being able to lay out a roadmap that allows you to understand the usefulness of entanglement in higher-level systems is a fundamental solution in quantum information science,” said Holland.
Looking at Multiple Dimensions
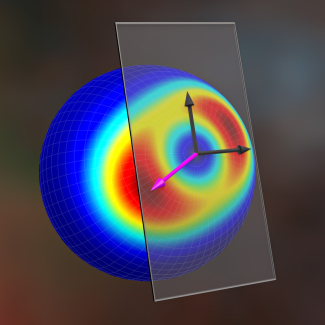
Most theoretical physicists researching quantum information science (which includes quantum sensing) focus on a system known as a qubit or “quantum bit,” graphically represented by a Bloch sphere or a 3D visual representation of all possible states of a qubit. A qubit is considered an SU(2) system where SU(n) is a simple way to mathematically describe how things in the quantum world can change and interact by exploiting the system’s symmetry. A qubit is considered an SU(2) system as it has a symmetry between two quantum levels, but as the number of levels go up, so does the SU(n).
Because these SU(n) systems can describe quantum entanglement, things get complicated quickly when n increases, as the system can exhibit multiple dimensions or ways that properties like entanglement can change in a multi-state system.
“You can think of the SU(n) system as putting a bunch of dots on a piece of paper and drawing a red, blue, and green line between these dots,” explained Jarrod Reilly, one of the paper’s first co-author and a graduate student in Holland’s group. The dots represent the different quantum states, while the lines highlight how the states “interact” with each other.
Instead of studying the SU(2) system with two distinct states (also known as degrees of freedom), Holland and his team looked at the SU(4) system, which describes four independent states. When studying the SU(4) setup, the researchers realized they were dealing with a mind-boggling 15 dimensions for how entanglement and other properties could change in the system!
Quickly, the team understood that a simple brute force calculation for the best use of the SU(4) system’s entanglement would be nearly impossible. “We had these states in this four-level system that were super complicated; we had no way of visualizing it,” elaborated John Wilson, a graduate student in the Holland group and the paper’s other first co-author.
To make it easier to calculate the QFI for these 15 dimensions, the researchers created an algorithm utilizing the QFIM, resulting in the best possible QFI value for the system. “We've come up with a method using the Quantum Fisher Information Matrix which says, here is the set of quantities for a given complicated state; these are the quantities that the state carries the most [useful] information about,” added Wilson.
Mathematical Shortcuts to Usefulness
Thanks to this algorithm, scientists have a type of “shortcut” that can give them the values of usefulness for more complicated systems without having to entangle them experimentally.
“If you have an experiment with complicated physics, you don’t need a full model to pull out how entanglement in the sensor could be used.” elaborated Holland. “To test if it's a good sensor, you only need to know the underlying symmetries of what you want to sense.”
The other benefit of this new algorithm is that it can work on almost any complicated quantum setup, making it useful for physicists in advancing current levels of quantum sensing technology.
Reilly elaborated that the algorithm works as an optimization problem. As an illustration, Reilly explained that if you were hypothetically trying to find the steepest part of a hill—which Reilly highlighted could have 15 dimensions—to roll a ball down, you could use the algorithm to calculate this solution without checking each direction.
“The algorithm leverages an underlying connection between quantum information (via entanglement) and geometrical concepts from Einstein's theory of relativity, two pinnacle fields of physics that rarely interact in research,” Reilly added.
While previous research has looked at measuring the QFI of quantum entanglement from a state-first perspective (where the sensor was created first, and then the entanglement was generated), this paper is one of the first to take the opposite approach.
“We can generate these classes of states, so we ask ourselves, what could we build with it?” Holland added. “It’s a new approach to understanding this whole sensing domain and a compelling method for quantum metrology.”
Written by Kenna Hughes-Castleberry, JILA Science Communicator