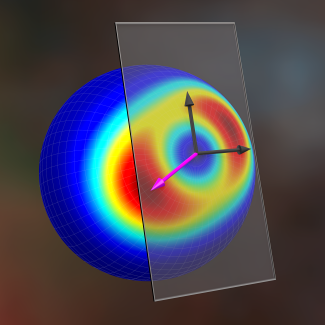
A schematic of the algorithm to find the optimal generator for a quantum sensing protocol. The quantum state can be mapped to a Lie algebra with a geometrically structure. The pink arrow represents the rotation axis which encodes the parameter that the state is most sensitive to, which simply corresponds to an eigenvector of the quantum Fisher information matrix.
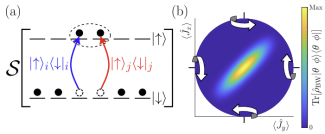
(a) Pair production that symmetrically drives entanglement between particles. (b) Two-axis countertwisting to create a Berry-Wiseman phase state which maximizes the information gained after a single measurement.
Historically, advancements in precision measurements have continuously propelled the scientific community’s understanding of the fundamental nature of reality. Currently, quantum optic-based sensing devices are pushing the frontier of precision measurement beyond what was achievable in the past, such as the Cornell/Ye lab’s electron EDM measurements at JILA surpassing those made in far more expensive particle accelerator experiments. This has led to revolutionary technologies like the Ye lab’s atomic clock and the LIGO and VIRGO gravitational wave detectors. However, most precision metrology experiments still operate using uncorrelated quantum states whose achievable sensitivity is fundamentally bounded by a classical limit.
In the Holland group, we propose experimentally relevant schemes to overcome this classical limit by generating metrologically useful quantum entanglement between the constituent particles of a given sensing device. The group analyzes the metrological use of quantum states with experimentally relevant techniques like Bayesian reconstruction, as well as more theoretical metrics such as the quantum Fisher information matrix. We have collaborated with the Rey theory group and Thompson lab at JILA to produce the first experimental realization of momentum entanglement in a vertical cavity setup. While the group primarily focuses on cavity QED platforms to entangle atoms, many procedures are more broadly applicable to various other nonlinear systems such as phonon-mediated trapped ion interactions, long-range BEC interactions, and spin-spin interactions in solid state materials. Our group has produced pioneering work on finding the optimal generator for sensing given any quantum state, where concepts from General Relativity fuses with quantum optics theory due to the geometrical properties of the underlying Lie group symmetries. This work opens the door to developing sensing protocols in systems where the constituent particles are not restricted to two-level systems, launching a new avenue to develop quantum sensing in more complicated systems in which entanglement is easier to generate and maintain.