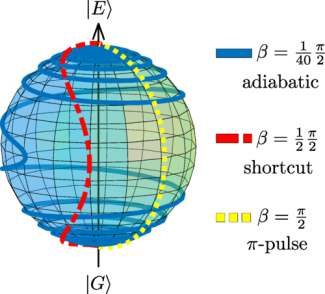
Bloch sphere trajectories comparing traditional population inversion schemes to the adiabatic shortcut. The shortcut takes a path that is much faster than the adiabatic path, but more robust to errors than simple π-pulses. This scheme was used to construct intensity and frequency profiles to speed up narrowline particle slowing protocols.
J. Bartolotta, J. Reilly & M. Holland, PRA 102, 043107 (2020)
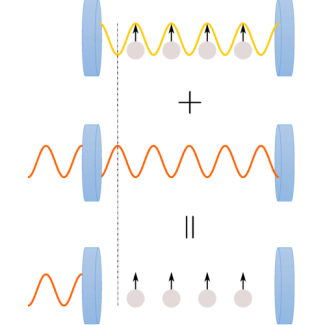
A sketch of engineering a dark state inside of a dissipative cavity. If the injected field is tuned such that it deconstructively interferes with the emission pattern of the atoms, the resulting system is a decoherence-free subspace in an open collective system, and is also effectively a perfectly reflective mirror for the external driving light.
The control of quantum systems is at the core of many groundbreaking scientific advancements. These quantum technologies often rely on state preparation that may require the generation of entanglement between specific elements of the system which is, in effect, quantum state engineering. This has become possible with the use of ultracold atoms, molecules, and ions, and the use of state-of-the laser technologies that drive highly controlled light-matter interactions. However, these experiments are, in reality, never entirely decoupled with the surrounding environment. Therefore, the performance of quantum state engineering protocols is often significantly reduced by dissipative effects, such as the electron’s interaction with the free-space electromagnetic modes leading to spontaneous emission.
To combat these issues, our research group studies quantum state engineering in the context of open quantum systems. Our work in this area explores two distinct pathways to deal with dissipative effects. For one, we are interested in schemes that speed up the system dynamics such that the state engineering occurs on a timescale much faster than that of the main dissipative effects. In the context of spin squeezing, exploring schemes in higher dimensional systems offer this possibility as it can avoid the coarse-graining criteria of adiabatic elimination calculations that reduce the system to highly studied two-level models. Another avenue for speeding up system dynamics is to avoid the requirement of adiabaticity which is usually employed to dynamically follow the eigenstates of time-dependent Hamiltonians. Such schemes are studied in the emerging field of adiabatic shortcuts, which our group has explored in the context of speeding up adiabatic passage. These shortcuts aim to transform systems from an initial quantum state to the same final quantum state as an ideal adiabatic process, but in much less time. They have also been shown to be more robust to other imperfections in experimental implementations such as intensity of frequency fluctuations of a driving laser. We have used an adiabatic shortcut based on Lewis-Riesenfeld invariant theory to construct the laser frequency and intensity profiles for a quick and robust particle slowing scheme.