Topological states of matter are a particular class of non-Landau states, which are characterized by the notion of topological order. For example in the fractional quantum Hall effect, the topological order is directly responsible for the celebrated properties of fractional charge, anionic statistics and gapless chiral edge modes. A major reason for the current interest in topological states of matter stems from the potential application of topologically protected quantum computation. For that, however, Abelian anionic statistics is not enough and instead one needs non-Abelian exchange statistics.
A prominent experimental candidate for this physics is the √ = 5/2 Fractional Quantum Hall (FQH) state. Nevertheless, up to date its non-Abelian nature has not been verified in experiments. A more exotic class of states which are predicted to support topological order and unusual gapless excitations are the so called quantum spin liquids. Quantum spin liquids have non-magnetic ground states even at zero temperature. Finding clear-cut examples in real materials of quantum spin liquid behavior has been also a challenge since most models and materials have magnetically ordered ground states. Cold atom realizations of topologically ordered materials and in particular quantum spin liquids will certainly be a breakthrough in modern quantum physics.
Our group is working in various ways to achieve these goals:
Synthetic gauge fields and optical flux lattices
The realization of quantum Hall states via synthetic gauge fields generated by a spatially dependent optical coupling between internal states of the atoms is becoming a very promising direction thanks to recent experimental progress.
AEA have been pointed out to be ideal for synthetic gauge field implementation thanks to the possibility of generating anti-magic lattice potentials –in which the clock states feel exactly the same lattice but with an opposite sign– and the fact that the long lifetime of the excited state reduces spontaneous emission. However, this is only at the single particle level. Recent measurements have revealed short life time of the excited states due to two body lossy collisions . One current recent topic in my group is on how to suppress or control such collisional relaxation as well as alternative ways of generating strong Abelian and non-Abelian gauge fields.
Alkaline earth atoms might realize the long-sought chiral spin liquid.
Quantum spin liquid phases in SU(N) systems
Magnetic frustration emerges from the inability to simultaneously satisfy a set of competing interactions and can be geometrical in origin or induced by strong quantum fluctuations. The latter are enhanced in systems with enlarged SU(N) symmetry. Recently in collaboration with colleagues at the University of Colorado we have pointed out that one of the simplest AEA quantum magnetic systems (a Mott insulator), on a two-dimensional lattice, is likely to realize the long sought chiral spin liquid (CSL) exotic phase. The CSL is a quantum magnetic analog of a FQH liquid, and has similar properties. Our preliminary calculations seem to indicate that the initial entropy required to observe such type of phases is more favorable than the one required to observe quantum magnetic ordering in SU(2) systems but nevertheless still hard to reach in current experiments. Since the underlying origin of the spin liquid behavior emerges from the large quantum fluctuations in SU(N) symmetric models, we are looking for alternative Hamiltonians and lattice geometries in which the entropy requirements are less restrictive.
a) Kitaev's honeycomb lattice. b): Compass-like model implemented using the shown level structure in polar molecules.
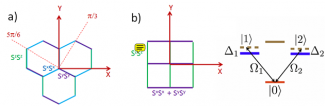
The implementation of highly non-trivial and anisotropic models such as the Kitaev honeycomb model and Yao-Kivelson triangle-honeycomb model is another way to generate topological matter. The practical realization of this type of models has been hindered by the fact that the interactions must be chosen in a very specific way, with spin degrees of freedom tied to the lattice directions. There have been previous proposals to realize the Kitaev model using alkali atoms however, they require complex laser set ups. Our recent work in polar molecules suggest that by properly choosing the rotational states and the microwave fields, one could implement dipolar interactions with angular dependence different from the typical (1 - 3 cos2 θ).
We are exploiting such flexibility to generate different anisotropic exchange interactions along the different directions which might facilitate the implementation of molecular analogs of various types of topological models such as the ones just mentioned. Systems exhibiting dipole-dipole interactions with non-trivial angular dependence could also be an alternative route to generate effective spin-orbit couplings, with the spin encoded in the rotational states of the dipoles. The underlying physics is similar to the so called Einstein de Haas effect by which an initial magnetization of an object can cause it to rotate mechanically or viceversa. Furthermore, we expect these ideas should be extendable to Rydberg atoms.