Trip across the Universe at constant acceleration
Suppose you took a trip across the Universe in a spaceship,
accelerating all the time at one Earth gravity \(g\).
How far would you travel in how much time?
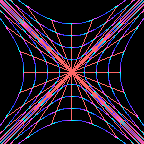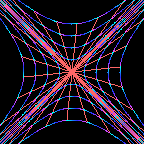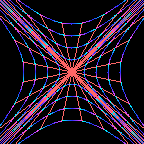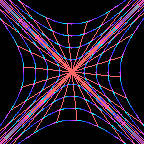
 The spacetime wheel offers a cute way to solve this problem,
since the rotating spacetime wheel can be regarded as representing
spacetime frames undergoing constant acceleration.
Specifically,
points on the right quadrant of the rotating spacetime wheel represent
worldlines of persons who accelerate with constant acceleration
in their own frame.
If the units of space and time are chosen so that
the speed of light and the gravitational acceleration are both one,
\(c = g = 1\),
then the proper time experienced by the accelerating person
is the boost angle
\(\alpha\),
and the time and space coordinates of the accelerating person,
relative to a person who remains at rest, are those of a point on
the spacetime wheel, namely
\(( t , x ) = ( \sinh \alpha , \cosh \alpha )\).
In the case where the acceleration is one
Earth gravity
\(g = 9.80665 ~ {\rm m/s}^2\),
the unit of time is
\[
{c \over g} =
{299{,}792{,}458 ~ {\rm m/s} \over 9.80665 ~ {\rm m/s}^2}
= 0.97 ~ \mbox{years}
\]
just short of one year.
For simplicity,
the table below takes the unit of time to be exactly one year,
which would be the case if one were accelerating at
\(0.97 \, g = 9.5 ~ {\rm m / s}^2\).
The spacetime wheel offers a cute way to solve this problem,
since the rotating spacetime wheel can be regarded as representing
spacetime frames undergoing constant acceleration.
Specifically,
points on the right quadrant of the rotating spacetime wheel represent
worldlines of persons who accelerate with constant acceleration
in their own frame.
If the units of space and time are chosen so that
the speed of light and the gravitational acceleration are both one,
\(c = g = 1\),
then the proper time experienced by the accelerating person
is the boost angle
\(\alpha\),
and the time and space coordinates of the accelerating person,
relative to a person who remains at rest, are those of a point on
the spacetime wheel, namely
\(( t , x ) = ( \sinh \alpha , \cosh \alpha )\).
In the case where the acceleration is one
Earth gravity
\(g = 9.80665 ~ {\rm m/s}^2\),
the unit of time is
\[
{c \over g} =
{299{,}792{,}458 ~ {\rm m/s} \over 9.80665 ~ {\rm m/s}^2}
= 0.97 ~ \mbox{years}
\]
just short of one year.
For simplicity,
the table below takes the unit of time to be exactly one year,
which would be the case if one were accelerating at
\(0.97 \, g = 9.5 ~ {\rm m / s}^2\).
Time elapsed
on spaceship
in years |
Time elapsed
on Earth
in years |
Distance travelled
in lightyears |
To |
|---|
|
\(\alpha\)
|
\(\sinh\alpha\)
|
\(\cosh\alpha - 1\)
|
|
| 0 |
0 |
0 |
Earth (starting point) |
| 1 |
1.175 |
.5431 |
|
| 2 |
3.627 |
2.762 |
|
| 2.337 |
5.127 |
4.22 |
Proxima Cen |
| 3.962 |
26.3 |
25.3 |
Vega |
| 6.60 |
368 |
367 |
Pleiades (Alcyone) |
| 10.9 |
2.7×104 |
2.7×104 |
Centre of Milky Way |
| 15.4 |
2.44×106 |
2.44×106 |
Andromeda galaxy |
| 18.4 |
4.9×107 |
4.9×107 |
Virgo cluster |
| 19.2 |
1.1×108 |
1.1×108 |
Coma cluster |
| 25.3 |
5×1010 |
5×1010 |
Edge of observable Universe |
After a slow start, you cover ground at an ever increasing rate,
crossing 50 billion lightyears,
the distance to the edge of the currently observable Universe,
in just over 25 years of your own time.
Does this mean you go faster than the speed of light?
No.
From the point of view of a person at rest on Earth,
you never go faster than the speed of light.
From your own point of view,
distances along your direction of motion are Lorentz-contracted,
so distances that are vast from Earth's point of view
appear much shorter to you.
Fast as the Universe rushes by,
it never goes faster than the speed of light.
This rosy picture of being able to flit around the Universe
has drawbacks.
Firstly,
it would take a huge amount of energy to keep you accelerating at
\(g\).
Secondly,
you would use up a huge amount of Earth time travelling around at relativistic
speeds.
If you took a trip to the edge of the Universe,
then by the time you got back not only would all your friends and
relations be dead,
but the Earth would probably be gone,
swallowed by the Sun in its red giant phase,
the Sun would have exhausted its fuel and shrivelled
into a cold white dwarf star,
and the Solar System, having orbited the Galaxy a thousand times,
would be lost somewhere in its milky ways.
Technical point.
The Universe is expanding,
so the distance to the edge of the currently observable Universe
is increasing.
Thus it would actually take longer than indicated in the table
to reach the edge of the currently observable Universe.
Moreover if the Universe is accelerating,
as recent evidence from the Hubble diagram of Type Ia Supernovae suggests
(Supernova Cosmology Project;
High-Z Supernova Search),
then you will never be able to reach the edge of the
currently observable Universe,
however fast you go.
|
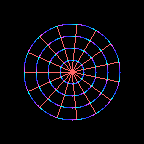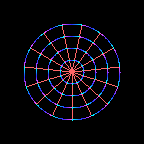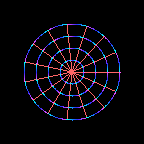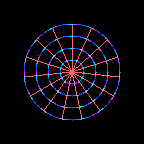 This is a wheel.
Each successive image in the movie is rotated by a small amount
compared to the previous image.
As the wheel rotates,
the coordinates
\(( x , y )\)
of a point on the wheel relative to its centre change,
but the distance \(r\) between the point and the centre
remains constant
\[
r^2 = x^2 + y^2 = \mbox{constant} \ .
\]
More generally,
the coordinates
\(( x , y , z )\)
of the interval between any two points in 3-dimensional space (a vector)
change when the coordinate system is rotated in 3 dimensions,
but the separation \(r\) of the two points remains constant
\[
r^2 = x^2 + y^2 + z^2 = \mbox{constant} \ .
\]
This is a wheel.
Each successive image in the movie is rotated by a small amount
compared to the previous image.
As the wheel rotates,
the coordinates
\(( x , y )\)
of a point on the wheel relative to its centre change,
but the distance \(r\) between the point and the centre
remains constant
\[
r^2 = x^2 + y^2 = \mbox{constant} \ .
\]
More generally,
the coordinates
\(( x , y , z )\)
of the interval between any two points in 3-dimensional space (a vector)
change when the coordinate system is rotated in 3 dimensions,
but the separation \(r\) of the two points remains constant
\[
r^2 = x^2 + y^2 + z^2 = \mbox{constant} \ .
\]