Cartwheel
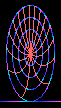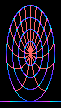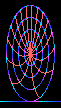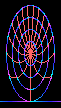 This is what a cartwheel looks like moving at 87% of the speed of light.
The cartwheel appears Lorentz contracted by a factor of 2
along the direction of motion.
The bottom of the cartwheel, where it touches the road,
is not moving, and is not Lorentz contracted.
You might think that the top of the cartwheel would have to move
faster than the speed of light to overtake the axle moving at
87% of the speed of light; but of course it can't.
The cartwheel offers another example of the impossibility
of completely rigid bodies in special relativity.
In the frame of reference of someone riding on the axle
(but not rotating),
the rim is whizzing around and is Lorentz contracted,
while the spokes are moving transversely, and are not contracted.
Something must give: the rim must stretch, or the spokes compress.
This is what a cartwheel looks like moving at 87% of the speed of light.
The cartwheel appears Lorentz contracted by a factor of 2
along the direction of motion.
The bottom of the cartwheel, where it touches the road,
is not moving, and is not Lorentz contracted.
You might think that the top of the cartwheel would have to move
faster than the speed of light to overtake the axle moving at
87% of the speed of light; but of course it can't.
The cartwheel offers another example of the impossibility
of completely rigid bodies in special relativity.
In the frame of reference of someone riding on the axle
(but not rotating),
the rim is whizzing around and is Lorentz contracted,
while the spokes are moving transversely, and are not contracted.
Something must give: the rim must stretch, or the spokes compress.
|
 At rest, the rocket is too long to fit inside one of the bays of the
International Space Station.
But at 87% of the speed of light,
the Lorentz contracted rocket
At rest, the rocket is too long to fit inside one of the bays of the
International Space Station.
But at 87% of the speed of light,
the Lorentz contracted rocket
 Of course from the rocket's point of view it is the Space Station
that appears Lorentz contracted, and there is even less room.
So what happens?
Of course from the rocket's point of view it is the Space Station
that appears Lorentz contracted, and there is even less room.
So what happens?