Falling to the Singularity of the Black Hole

Falling to the singularity of the black hole (217K GIF movie). This is the same movie as on the index page.

Clicking on the image gives you a double-size version of the same movie (same 217K GIF, same resolution, just twice as big on the screen).

\(1.5\) Schwarzschild radii from the singularity.

This is the location of the innermost unstable circular orbit. To maintain circular orbit at this radius requires going at the speed of light. In particular light itself can orbit the black hole in circular orbits at this radius. For this reason, this location is sometimes called the photon sphere.

Inside \(1.5\) Schwarzschild radii, no circular orbits exist, stable or unstable: all free fall orbits fall into the black hole. To maintain orbit inside \(1.5\) Schwarzschild radii without falling in, it would be necessary to keep rockets constantly on burn.

Answer to the quiz question 1: False. Photons do not orbit in circles at the horizon, just skimming the surface. The place where photons orbit in circles is the photon sphere, at \(1.5\) Schwarzschild radii. Photons emitted at the horizon fall in; except that if a photon is emitted exactly vertically outward exactly at the horizon, then it will hover at the horizon, not moving at all.

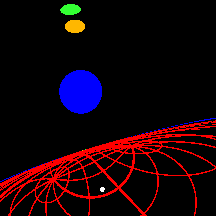At exactly \(1\) Schwarzschild radius, the horizon, the Schwarzschild surface. The point of no return.

An observer outside the black hole cannot see us beyond this point - we would appear to take an infinite amount of time to pass through, becoming slower and more redshifted as time goes by. But from our own point of view space and time continue normally.

The small white dot indicates our point of entry through the horizon. Remarkably, the Schwarzschild surface, the red grid, still appears to stand off at some distance ahead of us. The white dot is actually a line which extends from us to the Schwarzschild surface still ahead, though we only ever see it as a dot, not as a line. The dot-line marks the formation of the Schwarzschild bubble (see below), and our entry into that bubble. Persons who fell through the Schwarzschild surface at this precise point before us would lie arrayed along this dot-line. At this instant, as we pass through the horizon into the Schwarzschild bubble, we see all the other persons who passed through this location before us also pass through the horizon into the bubble.

The tidal force between head and toes is now \(1\) million gees, for this \(30\) solar mass black hole. But the tides wouldn’t be so bad for a very massive black hole. The tide at \(1\) Schwarzschild radius would be less than \(1\) gee if the black hole exceeded \(30{,}000\) solar masses.

From here to the central singularity will take \(0.0001\) seconds in free fall, for this \(30\) solar mass black hole. The infall time is proportional to the mass of the black hole.

Relative to an observer stationary in the Schwarzschild metric, our velocity has now reached the speed of light. Relative to an observer freely falling radially from rest at infinity, our velocity is \(\sqrt{8/9} \, c = 0.94 \, c\).

Answer to the quiz question 2: No, the horizon is not the place where you are suddenly torn apart. In a stellar-sized black hole like this one, the tidal force would already have torn you apart well outside the horizon. In a supermassive black hole the tidal forces are weaker, and you could survive well inside the horizon of the black hole before being torn apart.

Answer to the quiz question 3: To remain at rest just above the horizon, you would have to accelerate like crazy just to stay put. Radial distances measured in your frame are greatly stretched compared to radial distances measured by observers who go with the flow, so you’d have to pay out your fishing line a long way before it hit the horizon. The acceleration goes to infinity for something that attempts to remain at rest at the horizon, so the fishing line that passed the horizon would either break, or drag you in.

At \(0.95\) Schwarzschild radii, just inside the Schwarzschild surface.

Too late now — we’re inside the black hole, with no hope of exit. We are doomed to hit the central singularity in a finite time however we fire our rockets (but we are already dead anyway from the tides).

Here there are no observers stationary in the Schwarzschild geometry, i.e. stationary with respect to the distant stars. If there were such observers, we (on our free fall trajectory) would appear to them to move faster than the speed of light, and vice versa.

The Schwarzschild surface appears to split into two in a region around us. We seem to lie inside a bubble formed by the two surfaces. Looking outward, we see the Schwarzschild surface (white grid lines) we just passed through. If other observers fell through the surface after us, we could see them fall through here, and they would appear neither infinitely redshifted nor slowed.

Looking inward, we see the same Schwarzschild surface (red grid lines) apparently still ahead. Persons who fell through before us would continue to appear here. Already redshifted and slowed, such persons would continue to grow ever more redshifted and slow.

Persons who appear to us to be inside the Schwarzschild bubble have passed inside the horizon of the black hole. If they are sufficiently close to us, then we can communicate with them, but they must be close, for there’s not much time left before we hit the central singularity, not much time left for light signals to travel between us.

Through the screen formed by the outward Schwarzschild surface, we see more distant parts of the Schwarzschild surface from above, curved into our view by the gravity of the black hole.

We never get to see the central singularity. Nor do we see anyone else ever hit the central singularity.

At \(0.68\) Schwarzschild radii. The split region of the Schwarzschild surface grows.

If we see someone enter the Schwarzschild bubble through the upper (white) surface, then the moment of passage marks the instant when we see them pass inside the horizon of the black hole.

Answer to the quiz question 5: False. You do NOT see all the future history of the world played out. Once inside the horizon, you are doomed to hit the singularity in a finite time, and you witness only a finite (in practice rather short) time pass in the outside Universe.

In order to watch the history of the Universe unfold, you would have to remain outside the horizon, the Schwarzschild surface. One way to watch all the history of the Universe would be to stay just above the horizon, firing your rockets like crazy just to stay put. The Universe would then appear not only speeded up, but also highly blueshifted (probably roasting you in gamma rays), and concentrated in a tiny piece of the sky just above you.

Personally if I had all that rocket power available, I wouldn’t use it to hover just above the horizon of a black hole. I’d rather take a trip around the Universe. Thanks to special relativistic time dilation, I could travel vast distances in a modest time, at superluminal speeds — apparently faster than the speed of light.

Answer to the quiz question 6: False. You do NOT see the outside Universe concentrate into an ever diminishing patch of the sky above you, which finally disappears altogether as you pass into the horizon. This misleading notion appeared in Black Holes: The Ultimate Abyss, which was otherwise a wonderful show with beautiful graphics, broadcast on the Discovery Channel on 12 Oct 1997. What is true is that the outside Universe would concentrate into a small region above you if you hovered just above the horizon, firing your rockets like crazy to stay put. But fire your rockets how you will, the view of the outside Universe will not disappear once you are inside the horizon.

This is a redshift map of the distant sky corresponding to the previous image. Red colours indicate regions of the sky where distant stars (like the blue, green, and yellow stars) would appear redshifted, their spectra shifted to longer wavelengths. Other colours, from orange to violet, indicate regions of the sky where distant stars would appear blueshifted.

The main effect is a strong blueshift of photons coming from ahead. This is a special relativistic beaming effect caused by our near light speed motion.

The blueshifted region also appears concentrated towards the horizon. This is caused by tidal effects from the gravity of the black hole. Just as the tide stretches you vertically, and squeezes you about your middle, so also photons from both above and below you get redshifted, while photons from the sides get blueshifted.

Blueshifted parts of the sky would appear brighter, redshifted parts dimmer.

At \(0.35\) Schwarzschild radii. Compare this view to the unconventional view you would see if the Schwarzschild surface were attached to another Universe via a wormhole.

Images are being distorted by two effects: a tidal distortion from the gravity of the black hole, and a special relativistic beaming from our near light speed motion.

Just as the tidal distortion redshifts images from above and below, and blueshifts them about your middle, so also it tends to repel images from above and below, and concentrate them about your middle. At first, images appear distorted into a kidney shape. As the distortion grows, images become stretched and squashed into a doughnut shape about your waist.

Our near light speed motion concentrates our view ahead, by special relativistic beaming. Relative to observers freely falling radially from rest at infinity, our velocity increases towards the speed of light: the relativistic Lorentz gamma factor at radius \(r\) is \(1 + 2 r_s/r\).

At \(0.01\) Schwarzschild radii.

The tidal force continues to concentrate our view into a ‘horizon’ shape, while our near light speed motion further concentrates the view ahead.

The tidal force and our motion blueshifts photons from the outside world eventually to very high energies, which we would see as x and gamma rays.

At \(10^{-9}\) Schwarzschild radii: \(1\) millimeter from the singularity.

The tidal force has become so strong that all images are concentrated into a thin line about (what is left of) our waist.

As we approach the central singularity, the ride becomes very bumpy — the ultimate roller coaster. Small perturbations in tidal forces, caused by the presence of us and any other particles around, become greatly amplified in the final approach. The perturbations grow into violently oscillating tidal forces. Even a single infalling photon is enough to induce such oscillations.

Besides shredding our already torn apart bits into subatomic particles, the oscillating tides create photons and particle-antiparticle pairs out of the vacuum, producing a fierce environment.

The singularity: an infinitely convoluted point of infinite curvature.
What happens to space and time now? Do space and time end? No one knows. Presumably the answer has something to do with a hitherto unfathomed theory of quantum gravity... maybe superstring theory?