TDSE-SAE simulations versus TDDFT calculations

We have developed a reproducible ab-initio method to produce benchmark tests between time-dependent Schrodinger equation (TDSE) in the single-active-electron approximation (SAE) and time-dependent density functional theory (TDDFT) in the highly nonlinear multiphoton and tunneling regime of strong-field physics. As key to the benchmark comparison we have obtained an analytic form of SAE potentials based on density functional theory. Using these potentials we find remarkable agreement between the results of the two independent numerical approaches for the high-order harmonic yields in helium, demonstrating the accuracy of the SAE potentials as well as the predictive power of TDDFT calculations. Furthermore, an extension of the approach for SAE potential to diatomic molecules has been developed and applied.

R. Reiff et al., J. Phys. Commun. 4, 065011 (2020)
J. Heinz et al., Opt. Express 28, 25022 (2020)

Numerical Basis State Method

In this method we numerically obtain the energy eigenstates of the field-free Hamiltonian in a box on the grid. The solution of the full time-dependent Schrödinger equation, including the interaction of the system with the external field, is then expanded in this numerical basis and propagated in time. Some observables, such as transition probabilities, can be easily obtained with this method and even monitored at certain times during the interaction. The method has been applied to recently observed phenomena related to strong-field excitation of atoms and calculations of the nonlinear susceptibilities - in collaboration with X. Gao (Beijing Computational Science Research Center, China) and J. Li (Shanghai Jiao Tong University and Tsinghua University, China).

S.H. Chen et al., Phys. Rev. A 86, 013410 (2012)

A Virtual AMO Lab

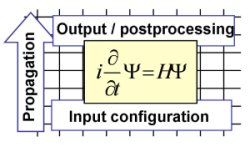In the nonperturbative intensity regime exact solutions of the time-dependent Schrödinger equation of a few-body system interacting with an ultrashort intense laser pulse can be obtained by direct numerical integration. Such simulations distinguish themselves just in the respective Hamiltonian of the Schrödinger equation. This is the basis of our program package, which provides an unified basis for a number of strong-field problems. It consists of routines for the propagation of the wavefunction on the grid and the post-processing of the data. The result is a virtual lab for the analysis and visualization of few-body processes on an attosecond time scale. Applications for single-active-electron as well as correlated electron dynamics have been realized.

Intense-Field Many-Body S-Matrix Theory

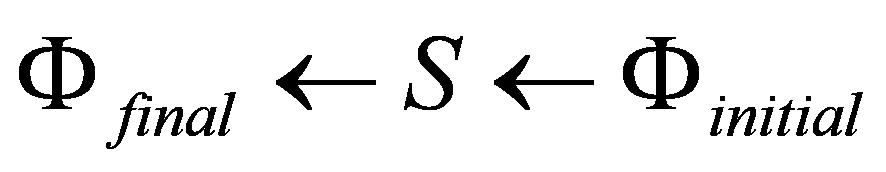The IMST provides a systematic ab-initio approach to investigate the dynamics of atoms and molecules interacting with intense laser radiation. Structurally, the usual S-matrix expansions, as the time-dependent perturbation theory, are based on a single partition of the total Hamiltonian of the system into an unperturbed reference Hamiltonian and the interaction potential. Such an 'one-potential' scheme is not very useful for the analysis of strong-field processes, in which the internal Coulomb interaction between the charged particles in the atom or molecule and the external laser-electron interaction energy are of comparable strength. Thus, one requires to be able to account simultaneously of different reference Hamiltonians in the initial, intermediate and final states. The IMST is such a more general S-matrix expansion scheme. It provides an effective method for analyses of direct and rearrangement processes that can occur in the presence of intense laser fields.

Review: A. Becker and F.H.M. Faisal, J. Phys. B 38, R1 (2005)