1. MAIN SEQUENCE STARS
In Lesson 4 we described how astronomers classify stars according to intrinsic properties [mass M, surface temperature T, luminosity L, radius R] and plot these properties on diagrams relating pairs of these properties [L&T; M&L; M&R]. On such plots, more than 90% of the stars cluster in a thin band called the main sequence. If one of these properties -- say, M -- is specified, all other properties -- L, R, T, are also determined. Clearly, all these main sequence (M-S) stars have many things in common; the only reason they differ from each other is that they have different masses. Why is this true? It turns out that we can understand these relationships as the result of three basic physical principles.
In his famous 1920 article, The Internal Constitution of the Stars, Arthur S. Eddington described the three basic principles that form our modern understanding of the Sun and other main sequence stars. They are:
These three principles, expressed mathematically, are sufficient to explain all the observed properties of main sequence stars. We'll discuss them in turn.
Hydrostatic Equilibrium: This principle says that since M-S stars are neither expanding nor contracting, there must be a nearly exact balance between the outward pressure force of the hot gas within the star and the inward tug on the gas due to gravity. Since scientists knew (from laboratory experiments) how pressure depends on gas density and temperature, and how gravity depends on mass and radius, they could write an equation setting these forces equal. From this equation, they could infer the central temperature of a star from its mass and radius. The result is:
Note that Tc is much hotter than the surface temperature of the star. For example the Sun (with Tc = 1.5 x 107 K) has a surface temperature of about 6,000 K.
With this equation and the observed mass-radius relation, we can deduce a very important clue to the structure of main sequence stars. The observations (see Lesson 4) show that main sequence stars have radius that is almost proportional to mass: R = M0.8. Plugging this observed fact into the above equation for central temperature gives the equation Tc = (1.5 x 107 K) M0.2, which implies that the central temperature of a main sequence star is extremely insensitive to the star's mass. For example, a blue giant star with mass M = 100 Solar masses will have Tc = 4 x 107 K, while a red dwarf with mass M = 0.1 Solar masses will have Tc = 1.0 x 107 K. While M ranges over a factor of 1000, Tc ranges over a factor < 4!
There must be a reason why all main sequence stars have almost the same central temperature!
Energy Transport: this principle describes how the tremendous heat energy in the interior of a star leaks out as the radiation we observe. Again, the appropriate equation follows from laboratory experiments. At the enormous temperatures inside stars, most of the radiation is X-rays. But even by 1920, people had been measuring how X-rays pass through matter -- specifically, how far X-rays could travel before they are absorbed or deflected by atoms. Eddington refers to these experiments in The Internal Constitution of the Stars.
Because the stars are so dense in their centers, radiation moves through matter by diffusion, or random walk, rather than simply streaming through it in straight lines like the light in the classroom. Each photon is scattered by atoms in random directions many times, and it will take much longer to escape from the center of the star than it would if it could travel out directly. For example, a photon would require only two seconds to travel from the center of the Sun to the surface if it could travel freely. But actually, it takes several thousand years for a photon to leak out of the Sun by diffusion. A good analogy is trying to cross the hall full of people - if you have to squeeze through a dense crowd, it would take you much longer to cross the hall than the time you would take to simply run across it if it were empty.
The experiments showing how X-rays pass through matter and a
theory for diffusion are sufficient to determine the luminosity of a main sequence
star from its mass, radius, and central temperature, i.e., to determine the
mathematical function L(M,R,Tc).
Moreover, since the principle of hydrostatic equilibrium gives Tc(M,R),
and we can determine Tc
from the observed mass-radius relation, the mass alone is sufficient to determine
the luminosity, i.e., these relations give the mass-luminosity relation L(M).
In fact, this theory gives the formula:
Massive main sequence stars are much more luminous than the Sun for two reasons: (1) the gas inside massive stars has lower density, so the radiation can leak out more easily; and (2) the massive stars have much greater volume, so they contain much more radiation which can leak out. The fact that the theoretical mass-luminosity relationship agrees with the observed one gives us more confidence that we truly do understand how the heat leaks out of main sequence stars. Energy generation: we have already discussed the idea that the Sun derives its energy from nuclear fusion reactions in its core. Eddington understood that the energy that would be released by the fusion of four hydrogen atoms to form helium was hundreds of times greater than the Sun's internal heat energy. He realized that such fusion reactions must be going on inside the Sun; otherwise it would collapse in about 20 million years, as Kelvin and Helmholtz said.
But Eddington did not know how such reactions could take place. Indeed, he recognized there was an unsolved mystery. To quote from The Internal Constitution of the Stars: "But is it possible to admit that such a transmutation is occurring? It is difficult to assert, but perhaps more difficult to deny, that this is going on."
It would be another 30 years until this problem was solved. The solution was found in the 1950's by Professor Hans Bethe of Cornell University. Like many physicists of that time, Bethe had worked on the development of the atomic bomb and the hydrogen bomb, and so he knew a lot more about nuclear reactions than Eddington knew in the 1920s. In fact, the key insight about how nuclear fusion reactions could occur was provided by George Gamow, who was a Professor here at the University of Colorado. You will hear a lot more about Gamow later in this course. Bethe understood Gamow's theory of nuclear reactions and he also knew a lot of detailed experimental information about fusion reactions.
The reason that fusion reactions require such high temperatures to occur is that atomic nuclei repel each other very strongly by electrical forces. The nuclei cannot react with each other unless they come very close. This is unlikely enough for two nuclei; it would be virtually impossible for four hydrogen atoms to get close enough to stick together all at the same time. Therefore, Bethe understood that the fusion of hydrogen into helium must take place by a sequence of reactions in which other elements are formed as intermediate steps. He discovered two such sequences of reactions, both of which play a role in converting hydrogen into helium in main sequence stars. The first, which dominates in stars with masses comparable to the Sun and less, is called the proton-proton chain, which is illustrated below. Click here for a movie showing these reactions in sequence.
The second, which dominates in more massive main sequence stars, is called the CNO cycle. This reaction sequence is described here. Click here for another movie showing the CNO cycle. Bethe's work on nuclear reactions put the final piece in the puzzle of main sequence stars: why do they all have nearly the same central temperature? Remember, this result followed from the principle of hydrostatic equilibrium and the observed relationship between stellar mass and radius. Bethe showed why this should be so. He knew that the thermonuclear reactions that led to fusion of hydrogen into helium would be extremely sensitive to temperature. At temperatures less than 107 K, they won't go at all. One can regard this temperature as a kind of "kindling temperature," or minimum temperature required to initiate and sustain a reaction. Above the kindling temperature, say, at temperatures exceeding that in the center of the Sun, 1.6 x 107 K, the reactions will go extremely rapidly. Stability of Main Sequence Stars: This temperature sensitivity of thermonuclear reactions creates an elegant kind of thermostat that regulates the central temperature of main sequence stars, Tc, at a constant equilibrium value. If Tc rises above this value, the nuclear reactions pump heat energy into the stellar interior at a greater rate than the energy can escape by radiative diffusion. This extra heat energy causes the interior of the star to expand a bit, and this expansion actually causes the interior temperature to decrease a bit. But that reduces the rate of the thermonuclear reactions, which causes the temperature to drop back to the equilibrium value for which the thermonuclear energy production exactly balances the heat loss by radiative diffusion. As we shall see in the next lesson, not all stars are so stable. In dying stars, the thermostat can fail. Then, the star's core will explode, releasing all its nuclear energy in minutes rather than billions of years. A very big bomb, called a supernova. A main sequence star is a wonderfully balanced mechanism, and we can all be thankful for that. (Return
to course home page)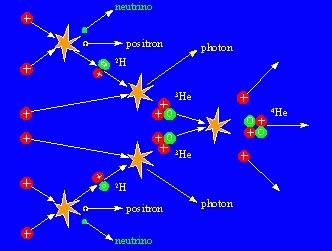
Last modified February 14, 2002
Copyright by Richard McCray