|
|
|
In a closed universe, light waves appear to converge. Source. |
Einstein's GTR is a theory of space, time, and gravity. In this theory, Einstein regards gravity as a manifestation of curvature of space and time. Think about a spherical surface, such as the Earth. The shortest distance between two points on the Earth's surface is a great circle (provided that you must travel close to the surface of the Earth, such as on an airplane). So, we may regard a great circle on a sphere as the analogue of a straight line on a plane. But great circles intersect. For example, if you travel from the North Pole to the South Pole by plane, the shortest route would be any meridian of longitude. No matter which direction you start out from the North Pole, if you fly straight ahead, you will eventually arrive at the South Pole. If two planes start out along two different meridians, they will get further and further apart; but after passing the equator they will converge again, finally meeting at the South Pole. If you didn't know that the Earth was round, you might think that there is some invisible force causing the planes to come together again. You might call it gravity.
|
|
|
In a closed universe, light waves appear to converge. Source. |
It turns out that three-dimensional space can be curved too. If two light waves (or photons) travel out from a quasar in different directions, they may first get further apart, but then converge again. We may regard this convergence of light waves as resulting from gravity, perhaps the gravity due to the mass of an intervening cluster of galaxies (see gravitational lenses). But Einstein regarded this gravity not as a force, but as a curvature of space and time. To be sure, the curvature is caused by the presence of matter. Here are the key ideas of the GTR: (1) the force of gravity should be regarded as a curvature of space and time; (2) objects (and light) move along the analogues of great circles in this curved space time; and (3) the curvature of space and time results from the presence of matter.
|
|
|
As the universe expands, the local curvature of space decreases. The distances between galaxies increase. The wavelength of radiation increases and its color shifts from blue to red. This is another way of regarding the red-shift of spectral lines from distant galaxies. Source |
Does this mean that we should forget about the force of gravity, and always think about the "curved space and time"? Of course not. When we feel the gravity of the Earth, we are indeed "moving" through the curved space and time (How do you think: are you moving if you stand still?). But for the vast majority of us, normal humans, 4-dimensional space-time is beyond imagination (with the exception perhaps of a few high-brained mathematicians, who can imagine a 4-dimensional world), and so we perceive our motion through the curved space and time as a force that acts on us. We call this force gravity. So, yes, the force of gravity is indeed a perception, but a rather real one - just try to jump off the second floor of a house! To express these ideas exactly (for example: exactly how do we describe a great circle in 4-dimensional space-time; and exactly what is the shape of curved space-time that results from the presence of matter) requires some fairly serious mathematics, which we won't go into here.
Actually, the easiest problem to solve using the GTR is that of the uniform universe. Einstein recognized immediately that if the universe contains matter, it must be curved. But if the universe is curved, all the matter must be in motion. In fact, according to Einstein's theory, the matter is not moving through space, the space itself is in motion. The universe must be either expanding or contracting.
I demonstrated the idea of a moving space by representing galaxies dots on an inflating balloon. The knots or dots are moving apart from each other. But they are not moving through the space (they are fixed on the rubber band, or on the balloon). The apparent motion is due to the expansion of the space itself. What does it mean to say "the space itself expands"? Imagine that somewhere deep in the empty space, far away from any star or galaxy, I put two small objects (say, two pieces of rocks) next to each other (say, one meter apart). Because my rocks are very far away from any star or galaxy, there is no external force that can affect them. The rocks are so small that their own gravity is miniscule. In this sense my rocks are "free" objects, i.e. objects that are not subject to any external force. Now, if I let these two rocks to sit in the empty space for a really long time (say, 10 billion years), I would notice (I must take care of my health really well, mustn't I?) that the rocks are moving away from each other. Again, there is no force that causes them to move away from each other, they move because the space itself stretches between them! But what about a piece of a rock itself? Does it get bigger because the space inside it also stretches? No. because the piece of rock is a solid object, its atoms are held together by the electromagnetic forces, and so atoms inside a rock are not free objects, so they slip as the space inside the rock expands, they are forced by attraction of nearby atoms to move through space (albeit veeeery slooooowly). For that same reason, the Earth, the Sun, the solar system, the Milky Way galaxy do not expand with the universe - they will have the same size billions and trillions of years from now (if they exist at that time, of course). So, remember this very well: only free objects participate in the expansion of the universe. Exert a force on an object, and you can make it move in whatever fashion you like. (Provided, your force is strong enough, of course!)
When Einstein realized that universe containing matter must be in motion, he couldn't believe his own theory! He thought that the universe must be unchanging in time, i.e., -- a universe with no motion, no beginning, and no end. This idea, that the universe is not only the same everywhere in space, but also in all time, is called the perfect cosmological principle. It wasn't based on any observation; it was just Einstein's preconception, or prejudice. And in fact, it's not right!
Once Hubble confirmed that the universe was expanding, most astrophysicists abandoned the idea of the perfect cosmological principle -- for the very good reason that if the universe is expanding, it must be thinning out, so that the density of galaxies is much less now than it was when the universe was much younger. But some very distinguished astrophysicists, notably Fred Hoyle, held on to the idea of the perfect cosmological principle in his theory of the steady state universe.
Therefore, instead of taking his solutions for the universe at
face value, Einstein modified his general theory of relativity (GTR) by introducing
a new term into his equations, which he called the cosmological
constant. It was represented by the symbol 
(Greek Lambda). It had the effect of a long-range repulsive force of space and
time that could counteract the attractive force of gravity. With the right choice
of ,
the solutions of Einstein's modified equations would permit a universe consistent
with the perfect cosmological principle.
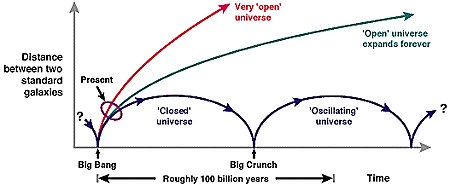
But meanwhile, Alexander Friedmann, a mathematician in St. Petersburg, Russia, had solved Einstein's equations for the universe without the cosmological constant. These solutions are called Friedmann solutions, which are illustrated above. You can see that there are actually two distinct types of solutions for the universe. All solutions start with a singularity, in which the distance between any two galaxies in the universe is compressed into a single point (which DOES NOT impliy that the entire universe is compressed to a single point! - can you think why?). One type of solution, called the closed universe, first expands, slows down, and then collapses again to a singularity. Then it might begin expanding again, in an endless succession of reincarnations, called the oscillating universe. (We're not actually sure that the universe will oscillate in this case. It may simply cease to exist after it collapses.) The other type of solution, called the open universe, expands forever. It has a definite beginning but no end. Actually, the diagram distinguishes between two types of open universes, a "very open universe", which expands forever, finally coasting at constant velocity, and an "open universe" which expands forever but is always decelerating.
Today, we believe that the Friedmann solutions accurately represent the past and future history of the universe. But which one of these possibilities is realized in reality? According to Friedmann's solutions of Einstein's equations, the answer to that question is determined by a quantity called W0, which obeys the equation W0 = r/rcr, where r is the actual average density of matter in the universe and rcr is the critical density of the universe, which is given by the equation
rcr = 3H02/(8 pG),
Actually, the question of whether the universe will expand forever or collapse again can be answered by a very simple argument that is familiar to anybody who has taken a course in physics. The key concept is called escape velocity. Escape velocity is the minimum velocity that an object must have in order to escape the force of gravity. For example, the escape velocity from Earth is about 11.2 km/s. If a rocket is launched straight upwards from Earth with velocity less than 11.2 km/s, it will fall back; but if it is launched with velocity greater than 11.2 km/s, it will escape the Earth's influence entirely and coast out into interplanetary space. Whether or not an object will escape from the influence of gravity is determined by two quantities: the amount of mass that attracts it back; and the speed of the object.
The escape velocity of any part of the universe is the minimum expansion velocity that it must have to escape the gravitational attraction of all the matter in that part of the universe. The speed of the universe is given by the Hubble constant (H0). The amount of mass is given by the average density of matter (r). Those two quantities are all we need know to determine W0 and, hence, whether the universe will expand forever or collapse again. The calculation is simple. You aren't required to know it, but you can find it here if you are interested: critical density. Plugging in the current value of the Hubble constant, we find that the value of the critical density is equal to about 5 hydrogen atomic masses per cubic meter.
Today, we can estimate the mass of dark matter in galaxies and clusters of galaxies in several ways: by the rotation curves of spiral galaxies; by the orbits of galaxies around each other in clusters; by gravitational lensing of galaxies in clusters; and by measuring the temperature and extent of X-ray emitting gas in clusters. (See Lesson 10). All these methods give similar answers: the mass of dark matter is about 10 times the mass of visible matter in the galaxies and clusters. If this ratio holds true throughout the universe, we can estimate that or W0 = 0.3 - 0.4, which implies that the universe will expand forever.
In Einstein's Theory of Relativity the space and time are not separate but are just two sides of one entity: the space-time. It is the space-time that is curved by matter and energy. And Friedmann's solutions connect the past and future evolution of the universe (time) with the curvature of space.
Because the universe is homogeneous and isotropic, there are only three possibilities for the space to be curved: it can be flat, like the surface of a table; it can be closed, like the surface of a sphere; or it can be open, like the end of a french horn. These three possibilities are illustrated below in a graph.
 |
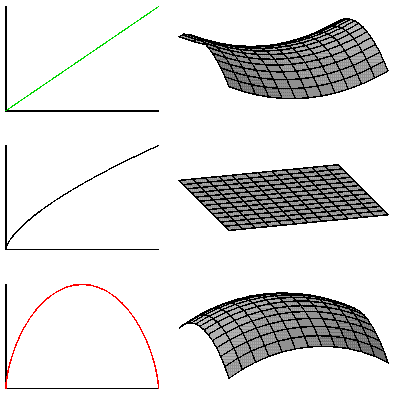Open geometry |
| Flat geometry | |
| Closed geometry |
The right column shows these three geometries, and the left column shows the fate of the universe that corresponds to each geometry*:
*This connection between the expansion history of the universe and the geometry of space is true for Friedmann's solutions, where the cosmological constant is zero. But if the cosmological constant is not zero, there are other possibilities. For example, the universe can have flat geometry but be speeding up. See ACCELERATION.
All Friedmann's models predict that the universe started in a state with infinite density and temperature. We know that in nature there are no infinities - the infinite density of the initial state simply means that even Einstein's theory of relativity is not valid for the very beginning of the history of the universe. And this is not surprising - after all, no physical theory explains everything; every theory has its own finite range of validity. Thus, with our contemporary body of knowledge we can only conclude that the universe was very dense and very hot at some early moment - what happened before that moment we do not know. And this moment we call the "Big Bang".
