11. ACCELERATION The cosmological constant returns:
Einstein called the cosmological constant his greatest blunder.
Why bring it up again? Mainly, because sometimes we encounter observations that
appear utterly inconsistent with the big bang model of the universe. But if
the cosmological constant is included in Einstein's equations, the solutions
allow a much greater variety of possible models for the cosmic expansion than
the Friedmann solutions. Just a few years ago, it seemed that there was a fundamental
contradiction between different measures of the age of the universe. At that
time, the Hubble constant seemed to be in the range 75 - 100 km/s/Mpc, implying
a universe with age less than 10 billion years today. Moreover, the best estimate
of the ages of the globular clusters was about 15 billion years. But you can't
have a universe younger than the stars in it! That would be a scientific crisis.
But with a cosmological constant, the universe could be older than 1/H0,
and the crisis would be resolved. Cosmologists are loath to include a cosmological
constant in their equations. It replaces a very simple set of solutions (the
Friedmann models) by a somewhat more complicated set. They would like the universe
to be simple. But if forced to choose between including a cosmological constant
or giving up the theory of the expanding universe, they'll include it.
Now, two recent observations have forced us to bring the cosmological
constant back into the picture. First, recent observations of distant supernovae
by two different groups indicate that the universe was expanding more slowly
when it was about half its present age than it is today -- i.e., the
expansion of the universe is accelerating,
not decelerating. (See Breakthrough
of the Year: Cosmic Motion Revealed and The
High-Z Supernova Search Team) The only way to have an
accelerating universe today is to have some kind of long-range repulsion in
the universe that overcomes gravity. That's exactly what a cosmological constant
does.
|

|
|
Very recently (April 2, 2001), astronomers using the Hubble Space
Telescope found a supernova with a redshift of 1.7 -- the most distant
supernova detected to date. The light from this supernova has been traveling
through intergalactic space for 10 billion years. Measurements of its
brightness indicate that the universe was still decelerating when the
light that we see today left this supernova, about 10 billion years
ago. But measurements of more nearby supernova indicate that the universe
has been accelerating more recently. Source.
|
In April 2000, new measurements of the fluctuations of the Cosmic
Background Radiation (CBR) have provided evidence indicating that there is a
cosmological constant. The idea is this: the curvature of the universe is determined
by the total energy density in the universe. The energy density is partly the
energy density due to the matter (most of which is dark matter) according to
Einstein's formula E = Mc2,
but also the energy density due to the cosmological constant, which astronomers
have begun to call "dark energy". The curvature of the universe can magnify
or de-magnify the fluctuations of the CBR at the epoch of recombination, as
illustrated below.
|
|
|
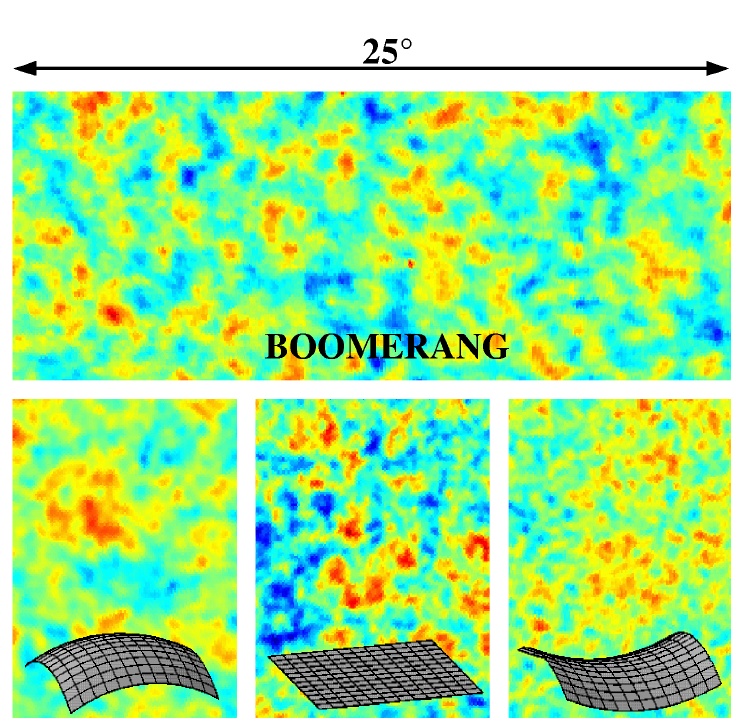
The curvature of the universe can be inferred from measurements
of the size scale of the angular fluctuations of the Cosmic Background
Radiation (CBR). A universe with positive curvature (lower left) will
magnify the size scale of the fluctuations, while a universe with negative
curvature (lower right) will de-magnify the scale. The observed fluctuations
(top panel) have a size scale in agreement with the prediction for a
flat universe (lower center). From the Boomerang
experiment.
|
The following diagram illustrates what the combined results
of the observations of distant supernova observations and the CBR tell us:
|
|
|
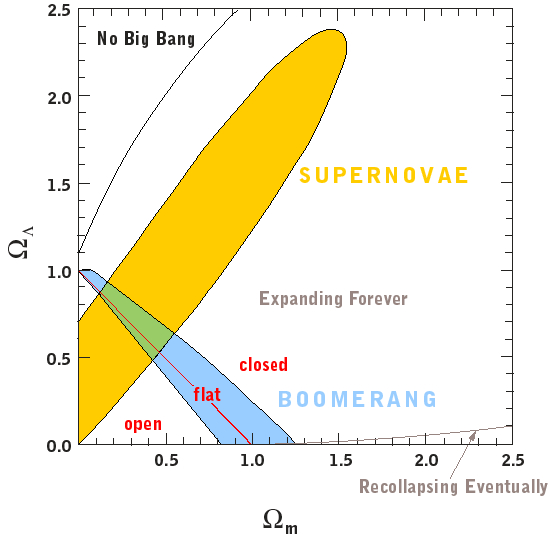
Combined results of measurements of the expansion rate of distant
supernovae (yellow wedge) and the angular fluctuations of the CBR (blue
wedge). The area of overlap (green) indicates possible models for the
universe that are consistent with both kinds of measurements. Source:
Boomerang.
|
In the diagram above, W
m is the closure parameter of the universe due to the dark matter,
which astronomers have determined has a value W
m = 0.3 - 0.4. W L
is a comparable measure of dark energy due to the cosmological constant. It
appears that the most likely values are W
m = 0.35 and W L
= 0.65, implying that the dark energy is about twice that of the dark matter
and that the universe is accelerating now.
|
|
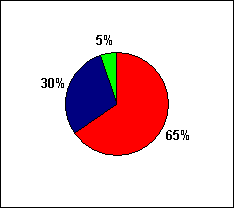
| The matter/energy content of the universe. The green wedge represents
ordinary matter, including stars and gas between the stars. The dark blue
wedge represents dark matter which, like ordinary matter, attracts. The
red wedge represents dark energy. |
The age of the universe, revisited: As
I mentioned at the top of this section, introducing the cosmological constant
changes the relationship between the age of the universe and the Hubble constant.
If the universe is accelerating now, it can be older than 2/(3H0).
In fact, the best current estimate of the age of the universe is
about 14 billion years (see Nick
Gnedin's Cosmological Calculator). This value is comfortably greater than
the age of the oldest stars.
What would Einstein think?
Einstein introduced the cosmological constant into his equations in order to
find a mathematical description of a universe that was static -- never changing,
no motion. To do that, he had to set the cosmological constant to have a value
exactly right to counteract gravity. But now we know that the universe is actually
expanding. Therefore, the cosmological constant that we need to describe the
actual universe today does not have the value that Einstein chose, and it does
not balance gravity. In fact, the acceleration due to the cosmological constant
exceeds the deceleration due to gravity. Evidently, Einstein introduced the
cosmological constant into his equations for the wrong reason, and so he chose
the wrong value. But the idea of the cosmological constant seems right today.
(Return
to course home page)
Last modified April 15, 2002
Copyright by Richard McCray