We investigate AMO (Atomic-Molecular-Optical) analogs of systems that fall under the general heading of quantum magnetism, where localized magnetic moments interact with one another and/or with mobile fermions. Important solid state systems in this class include the cuprate superconductors, heavy fermion materials, colossal magnetoresistive manganites, and geometrically frustrated magnetic insulators.
The Fermi and Bose-Hubbard models describe fermions and bosons hopping between adjacent lattice sites and interacting only when two particles are in the same site. The Fermi Hubbard model is believed to contain the minimal ingredients behind high temperature superconductivity. Major breakthroughs have been achieved towards the implementation of these models with ultra-cold atoms. Nevertheless, the actual observation of quantum magnetism in the Fermi/Bose Hubbard models has been hindered by the required low energy scales not currently achievable in experiments.
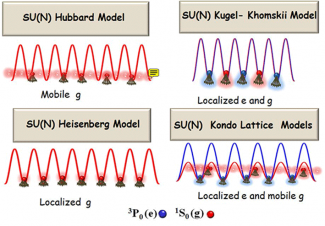
However, it should be emphasized that Hubbard-type models correspond to the simplest and crudest characterization of solid state materials. They assume particles are confined in a single orbital. Extending from those, there is a large list of more sophisticated and iconic Hamiltonians which rely on the interplay of the electron’s charge, spin and orbital degrees of freedom. This interplay is believed to be key in the understanding of the complex and novel behavior observed in real materials. The Kondo lattice model and the Kugel-Komskii model are two iconic examples.
The Kondo lattice model describes tightly bound electrons which act as spinful scattering centers for electrons in a conduction band. When the exchange coupling between the conduction and localized electrons is anti-ferromagnetic, it gives rise to a rich and still poorly understood phase diagram with magnetically ordered phases, heavy Fermi liquid phases, and unconventional superconductors. The ferromagnetic Kondo lattice model, on the other hand, has attracted much renewed interest due to the discovery of colossal magnetoresistance (huge change in the resistivity when an external magnetic field is applied).
The Kugel-Khomskii model is used to describe, for example, the Mott insulator phases in transition metal oxides with perovskite structure in which the electrons are localized in two orbitals.
These are some directions we are exploring towards the investigation of orbital magnetism with ultra-cold atoms.
Alkali atoms: Higher bands/Non-trivial lattice geometries
Alkali atoms have a relatively simple electronic structure which has allowed a clean characterization of their hyperfine levels and has facilitated the development of effective trapping and cooling methods. Major breakthroughs have been achieved with these atoms, such as the implementation of both repulsive and attractive Fermi and Bose-Hubbard models. Those require atoms to populate the lowest band in a lattice. Spin degrees of freedom can be incorporated by encoding the spin in internal hyperfine states.
A natural way to add orbital degrees of freedom is to populate higher bands in cubic or more complicated lattice geometries with a multi-site basis. One important limitation of using higher bands to probe orbital magnetism is that the occupation of such excited lattice bands is, at best, metastable. The latter is especially bad for bosons since they do not have the Pauli exclusion principle to block the population of already populated lower bands. Nevertheless, there should be ways to overcome this limitation. We have been exploring theoretically optimal ways to implement atomic analogs of the Anti-ferromagnetic and Ferromagnetic Kondo lattice models and the Kugel-Komskii model by populating higher bands. We have found that collisions between atoms in p-bands impose a serious constraint in the Kondo model implementation if one uses separable lattice potentials but that this limitation can be overcome by using already implemented non-separable lattices. Similar type of stability might be achieved with alternative routes.
We have also investigated how to engineer interaction-induced ferromagnetism in ultra cold sermonic atoms by populating higher bands of a checkerboard superlattice.
It is clear that the “simple” atomic structure exhibited by neutral alkali atoms actually limits the physics that can be investigated with them. Systems exhibiting more complex interactions and/or an enlarged set of degrees of freedom, with the same degree of controllability, can be an excellent alternative platform for exploiting a wider range of anybody phenomena. Among those are: Alkaline earth atoms, Polar molecules and Trapped ions. It should be also said that many of the trapping and cooling capabilities previously demonstrated with alkali atoms are starting to be reproduced in the systems mentioned above.
Alkaline earth atoms (AEA)
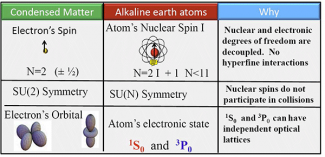
We investigate the use of sermonic alkaline-earth atoms (AEA)–atoms with two valence electrons - loaded in optical lattices as quantum simulators of unique many-body Hamiltonians beyond the one band Hubbard model. AEA possess a unique atomic structure consisting of a metastable excited triplet state coupled to the ground singlet state via an ultra-narrow doubly forbidden transition. The electronic singlet and triplet states (known as clock states) have both zero electronic angular momentum and have already demonstrated a great potential for optical frequency standards and clock technology. The basic idea that we first proposed is to exploit their unique atomic structure to simulate two-orbital-SU(N) Hamiltonians which rely on the interplay of charge, spin and orbital degrees of freedom. The clock states play the role of the orbital degrees of freedom and the corresponding nuclear spins provide the spin degrees of freedom. The SU(N) symmetry arises in the sermonic alkaline earth isotopes due to the independence of their scattering parameters on the nuclear spin. This is because in these atoms nuclear spins are fully decoupled from the electronic degrees of freedom.
The advantage of using AEA towards the implementation of orbital physics is that the two electronic clock states can feel independent optical lattice potentials, and in contrast to the spin mixtures, at the same time they can exchange their nuclear spins. In close collaboration with the condensed matter theory group at the University of Colorado we have started to explore some of the novel consequences of the SU(N) symmetry using different techniques such as large N expansions of the SU(N) Heisenberg model, DMRG studies and Bethe ansatz solutions of the one-dimensional SU(N) Hubbard model, and high temperature expansions of the SU(N) Hubbard model. We have also explored an implementation of the SU(2) antiferromagnetic (AF) Kondo lattice model using both clock states.
We are also developing theoretical principles underlying the identification, characterization and classification of distinct phases of matter in models such as SU(N) Heisenberg models, SU(N) Kugel-Komskii and SU(N) Kondo lattice models as well as theoretical guidance towards their experimental observation.
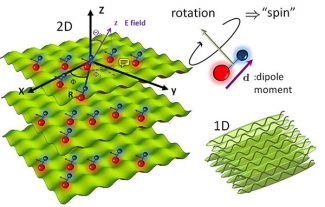
Ultracold polar molecules loaded on optical lattices: Arrays of 2D pancakes and arrays of 1D tubes. The rotational de- grees of freedom of the molecules is used as the effective spin degrees of freedom which interact via strong long-range and anisotropic direct dipole-dipole interactions. External dc electric fields and microwave fields are used as control knobs.
Polar Molecules
Diatomic polar molecules are another great example of more complex AMO systems. They possess a permanent dipole moment, which can be manipulated with external fields, and which can lead to long-range anisotropic interactions. They also exhibit a hierarchy of internal degrees of freedom including hyperfine, rotational, vibrational and electronic levels. Recently, impressive experimental advances have allowed the production of sermonic KRb polar molecules in their electronic, rotational, and vibrational ground states. The experimental ability to independently manipulate vibrational, rotational, and hyperfine levels has been also demonstrated.
One research thrust in our group is on the use of polar molecules to emulate orbital quantum magnetism. The focus is now mainly on alkali-dimers given their well characterized hyperfine structure and their close connection to current JILA experiments. The basic idea is to use the rotational degrees of freedom in the molecules, controllable by dc electric fields and continuous microwave fields, as the analogs of the spin degrees of freedom in electronic systems. Those degrees of freedom will be manipulated to realize complex long-ranged, anisotropic Hamiltonians via tunable and strong dipolar interactions. In our scheme the rotational degrees of freedom of the molecules are coupled by strong long-range and anisotropic spin exchange interactions generated by the direct dipole-dipole interaction between molecules. This is not the case in atoms where the net spin exchange interactions (super-exchange) are one or two orders of magnitude weaker.
We have discussed a possible implementation of a generalized version of the t –J model with polar molecules. We called it the t - J -V -W model. Furthermore, we have shown that by applying microwaves and dc electric fields one can generate richer types of interactions and engineer novel Hamiltonains such as : SU(N) Heisenberg models, anisotropic spin models possessing "symmetry protected topological" phases, and models with real topological phases such as the Kitaev model.
The first observation of quantum magnetism in polar molecules using our proposal has been recently done in the KRb polar molecule experiment at JILA. Dipolar exchange interactions has been resolved and controlled even at current conditions: in a dilute and non-degenerate polar molecule gas pinned in a deep optical lattice.
Trapped ions
Trapped ions have been shown to be fully controllable quantum systems with applications that range from time keeping and sensing, to quantum computing. Recently trapped ions have been also utilized as quantum simulators of spin models by encoding the spin in hyperfine degrees of freedom. At NIST-Boulder crystals of 100-500 ions have been used to engineer Ising models with fully controllable long range interactions. The spatial order comes from ion-ion Coulomb interactions. In those systems the spin interactions are created by applying spin dependent forces mediated by phonons. One main limitation for the observation of spin correlations in those systems is decoherence.
We are developing theoretical techniques to understand the interplay between interactions and decoherence and to guide experiments towards the best way to observe interesting many-body behavior.