|
Mathematical form of the Lorentz transformation
Mathematically, the form of the Lorentz transformations
illustrated pictorially above is as follows.
The units in these equations are
\(c = 1\),
following the convention for
spacetime diagrams.
Suppose that Cerulean (primed frame) is moving
relative to Vermilion (unprimed frame)
at velocity \(v\) in the \(x\) direction.
Then the coordinates
\(( t' , x' , y' , z' )\)
of an event in Cerulean's frame are related to
the coordinates
\(( t , x , y , z )\)
of the same event in Vermilion's frame by
\[
\begin{array}{l}
t' = \gamma t - \gamma v x
\\
x' = - \, \gamma v t + \gamma x
\\
y' = y
\\
z' = z
\end{array}
\ , \quad
\begin{array}{l}
t = \gamma t' + \gamma v x'
\\
x = \gamma v t' + \gamma x'
\\
y = y'
\\
z = z'
\end{array}
\]
These Lorentz transformation formulae can be written elegantly in matrix
notation:
\[
\begin{align}
\left(
\begin{array}{c}
t'
\\
x'
\\
y'
\\
z'
\end{array}
\right)
&=
\left(
\begin{array}{cccc}
\gamma & - \gamma v & 0 & 0 \\
- \gamma v & \gamma & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{c}
t
\\
x
\\
y
\\
z
\end{array}
\right)
\ ,
\\
\left(
\begin{array}{c}
t
\\
x
\\
y
\\
z
\end{array}
\right)
&=
\left(
\begin{array}{cccc}
\gamma & \gamma v & 0 & 0 \\
\gamma v & \gamma & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{c}
t'
\\
x'
\\
y'
\\
z'
\end{array}
\right)
\ .
\end{align}
\]
Any 4-dimensional quantity
\(( t , x , y , z )\)
that transforms according to the rules of Lorentz transformations, as above,
is called a 4-vector.
A Lorentz transformation at velocity \(v\) followed by
a Lorentz transformation at velocity \(v\) in the opposite direction,
i.e. at velocity \(-v\) yields the unit transformation, as it should:
\[
\left(
\begin{array}{cccc}
\gamma & \gamma v & 0 & 0 \\
\gamma v & \gamma & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{cccc}
\gamma & - \gamma v & 0 & 0 \\
- \gamma v & \gamma & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right)
=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right)
\ .
\]
The determinant of the Lorentz transformation is one, as it should be:
\[
\left|
\begin{array}{cccc}
\gamma & - \gamma v & 0 & 0 \\
- \gamma v & \gamma & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}
\right|
=
\gamma^2 ( 1 - v^2 )
=
1
\ .
\]
Indeed, requiring that the determinant be one provides another
derivation of the
formula for the Lorentz gamma factor.
|
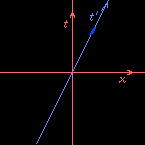
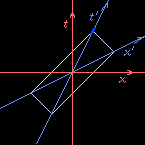
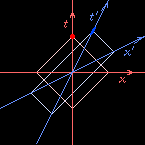
 Draw a spacetime diagram
(see the
The Paradox of Special Relativity
page for a definition)
from Vermilion's point of view.
For simplicity keep only one spatial dimension,
the \(x\) direction,
the direction of Cerulean's velocity relative to Vermilion.
The time \(t\) and distance \(x\) of events,
relative to the origin,
are those measured by Vermilion.
Draw Vermilion's worldline vertically through the origin,
and a horizontal “now” line, also through the origin.
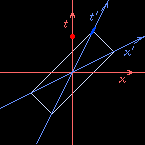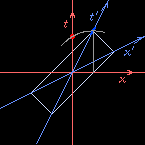
Draw a spacetime diagram
(see the
The Paradox of Special Relativity
page for a definition)
from Vermilion's point of view.
For simplicity keep only one spatial dimension,
the \(x\) direction,
the direction of Cerulean's velocity relative to Vermilion.
The time \(t\) and distance \(x\) of events,
relative to the origin,
are those measured by Vermilion.
Draw Vermilion's worldline vertically through the origin,
and a horizontal “now” line, also through the origin.