6. WHITE DWARF STARS 

After the AGB star has ejected its envelope as a planetary nebula, the star that remains is a very compact core of carbon/oxygen (perhaps covered with a thin layer of residual helium). What happens to this star?

As we have discussed, when the core of a star burns up all its fuel, it must begin to contract as it radiates away its heat energy. It contracts because the lost heat implies a loss of pressure support. Up to now, the only pressure that we have been considering is heat pressure. But at very high gas density, such as that encountered in the carbon/oxygen core of an AGB star, a new kind of pressure, called degeneracy pressure, becomes comparable to or greater than the heat pressure. As we shall discuss below, this degeneracy pressure stops the contraction of the carbon/oxygen core.

Degeneracy pressure is familiar to all of you. It is the pressure that prevents liquids and solids from being compressed. Squeeze on any solid object: it pushes back. Gas pressure is "squishy", as you can test by pumping your bicycle tire with a hand pump. But at a density of a few grams per cubic centimeter, ordinary matter becomes liquid or solid and is nearly incompressible. No apparatus on Earth can compress water (or steel) to half its volume. Moreover, the tendency of liquids and solids to resist compression is almost independent of their temperature. Liquids and solids do not shrink much when cooled, even to almost absolute zero temperature (-273 C). The same degeneracy pressure prevents atoms from collapsing.

Scientists gained a better understanding of this degeneracy pressure during the 1930s when they developed theory of quantum mechanics, which explains the structure of atoms, molecules, and liquid and solid matter. With this theory, we can understand how matter at high density resists compression.

The theory tells us that it is possible to compress matter, even at very high density, but that the necessary pressures are enormous. For example, even at the center of Earth the iron is only compressed by about 10% in volume. But at the center of Jupiter the pressure is sufficient to compress the matter by almost a factor of 2. The density in the carbon/oxygen core of an AGB star (or the central star of a planetary nebula) is so great that this degeneracy pressure becomes greater than the heat pressure. But since degeneracy pressure doesn't require heat energy, it doesn't diminish when the carbon/oxygen core radiates away its heat. That means the star doesn't shrink anymore -- it simply cools off.

If the carbon/oxygen star has mass less than 1.4 solar masses, it has come to the end of its life story. It has no nuclear reactions and it will have no further major structural changes. It will take many millions of years, however, before it cools off enough that it becomes invisible. We call such a star a white dwarf star.

As the white dwarf star cools, the carbon atoms will crystallize into diamond. Think of it: a single diamond with a mass equal to 300,000 times the entire Earth! But don't count on getting rich mining these diamonds. The gravity on the surface of a white dwarf star is something like 300,000 times the gravity on Earth, and you would weigh 30 million pounds there. Better just enjoy the thought that billions of such diamonds really exist.

In fact, astronomers have discovered many white dwarf stars. Indeed, the brightest star in the sky, Sirius, is actually a binary system consisting of Sirius A, a main sequence star (mass about 2.5 Suns), and Sirius B, a white dwarf. The radius of Sirius B, as inferred from Stefan's Law (see Lesson 4), is actually less than the radius of Earth. We know now that there are billions of white dwarf stars in the Milky Way galaxy, but we haven't observed very many because they are so faint and hard to find.

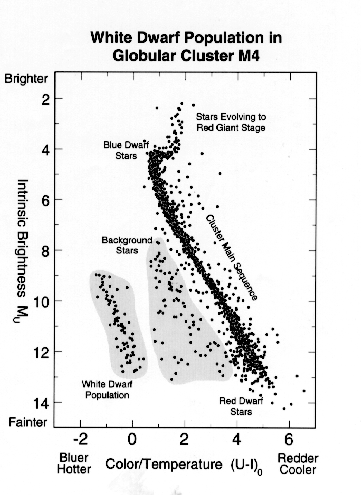
Astronomers believe that all stars with initial masses less than about 7 Solar masses will end up as white dwarf stars. Therefore, they expected that globular clusters would contain many white dwarf stars (because they are billions of years old and have no main-sequence stars more massive than the Sun). But globular clusters are very distant, and until recently it was impossible to detect the very faint white dwarf stars within them. But now, the Hubble Space Telescope has observed many white dwarfs in the globular cluster M4. Below is a color-magnitude diagram of M4, showing the faint main sequence and white dwarf stars detected there (this diagram does not show the brighter red giants and horizontal branch stars in M4).

The theory of the structure of white dwarf stars was first worked out in 1930 by S. Chandrasekhar while he was a graduate student at Cambridge University. Chandrasekhar's theory showed that a white dwarf star with mass equal to that of the Sun would have a radius less than that of the Earth. That implies that the average density of such a star would be greater than a million times the average density of the Earth -- a one ounce shot glass of white dwarf matter would weigh more than 100 tons! For more details of the physics of white dwarf stars, look here.

Chandrasekhar's theory also showed that the greater the mass of such a star, the smaller its radius would be. In fact, he found that if the star's mass exceeded 1.4 times the Sun's mass, the degeneracy pressure would not be strong enough to resist gravity and the star would collapse. We call this value of mass -- 1.4 Suns -- the Chandrasekhar limit*. As you will see, this limit plays a fundamental role in determining the final fates of stars.

*Arthur S. Eddington, also at Cambridge University, didn't believe this result, and in fact ridiculed the idea. But he was wrong.

Actually, planets, such as Earth and Jupiter, are also supported by degeneracy pressure, so their structure is related to that of white dwarf stars, as illustrated by the blue curve in the mass-radius diagram below.

The axes of this diagram are labeled in logarithmic scale so that, for example, Jupiter, with mass = 10^-3 solar masses and radius 60,000 km, has Log(Mass/Solar Mass) = -3 and Log(Radius/kilometers) = 4.8. The blue curve shows the relationship between mass and radius for objects held up by degeneracy pressure (planets and white dwarf stars). One sees that the matter in planets lighter than Jupiter is almost incompressible, so that the radius increases with increasing mass. But in planets with masses greater than Jupiter's, the central pressure is so great that the matter there is compressed significantly. Jupiter is almost as big as a planet can be. If one could somehow shovel matter onto its surface, Jupiter wouldn't get much bigger. In fact, a planet with mass ten times that of Jupiter would actually be smaller than Jupiter, and Sirius B (a white dwarf), which has mass about equal to the Sun, is smaller than the Earth! Note also that the blue curve turns down vertically at Log(Mass/Solar Mass) slightly greater than 0 (i.e., at M = 1.4 Solar Masses), the Chandrasekhar Limit. That means that a white dwarf with mass greater than this value will collapse. The green line on this mass-radius diagram represents the mass-radius relationship for main sequence stars. As we described, these stars are supported by heat pressure, not degeneracy pressure, and the relationship represented by the green line is a consequence of the fact that main sequence stars all have nearly the same central temperature. This line terminates at a mass of about 200 Suns, above which no stable main sequence star can exist (we think!). (We'll return to this diagram later to discuss the lines labeled "neutron stars" and "black hole limit".)

(Return to course home page)
Last modified February 25, 2002
Copyright by Richard McCray