4. SPECTRAL TYPE
The third obvious property of a star is its color. As a first approximation, a star radiates a blackbody spectrum. Therefore, according to Wien's Law (see
Lesson 1), the true color of a star depends on the temperature of the star's photosphere*: a hot star (say, 20,000 K) appears blue, while cool star (say, 3000 K) appears red. We can use this fact to determine the temperature of a star by choosing the temperature of a blackbody spectrum to make the best fit to the spectrum of an actual star, as illustrated by this Blackbody Applet (from the University of Oregon).
*
The photosphere is the "surface" of the star, where the light finally emerges. Since the star is gaseous, the photosphere is not a hard surface, but a diffuse layer. The temperature of a star's photosphere can be very different from the temperature of the star's interior.
But, the observed color of a star is an extrinsic property because, as we have already noted, starlight may be reddened if it passes through intervening dust. The dust will preferentially absorb the blue light from the star, making the star appear redder than it actually is. Since there is very little interstellar dust within a few hundred light years of the Sun, the observed color of a nearby star will be nearly the same as its actual (intrinsic) color. But the situation is more complicated with distant stars. A distant red star may be cool, or it may actually be a hot blue star that appears red because its blue light is absorbed by intervening dust. How can we tell whether a red star is actually cool, or only appears red because of the dust?
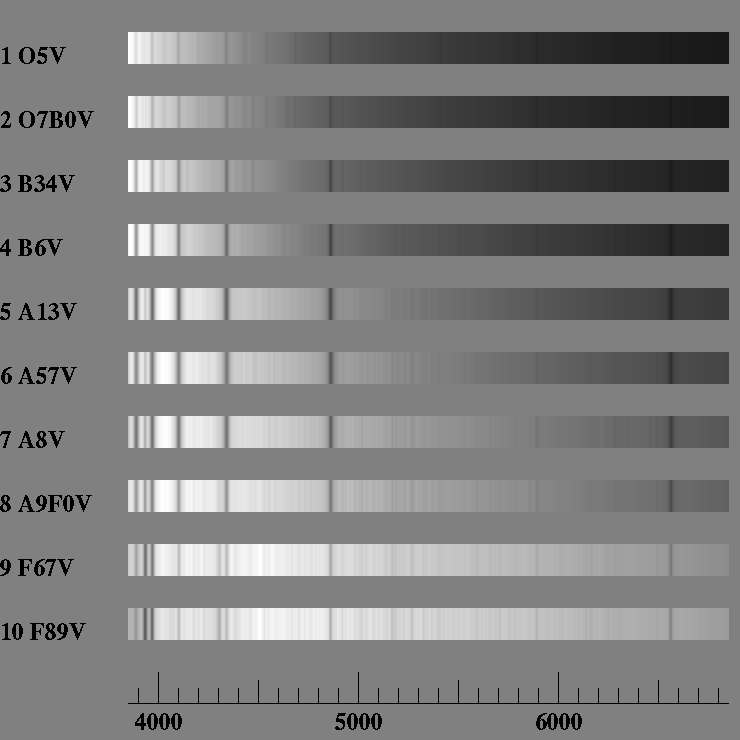
Astronomers have a far more accurate method of measuring the temperature of a star's photosphere than by measuring colors. That is to measure the star's spectrum, which contains hundreds or thousands of spectral lines of different atoms and molecules. The presence or absence of certain spectral lines of an atom depends not only on the abundance of the atoms, but also on the temperature of the gas. Take helium, for example. It takes a lot of energy (heat) to excite the electrons in helium atoms. Therefore, we can't see any lines due to neutral helium in the star's spectrum unless the gas in the photosphere has a temperature T > 15,000 K, and none due to ionized helium unless T > 25,000 K (see below). Likewise, we can't see any spectral lines due to molecules unless T < 4500 K. By analyzing the ratios of the strengths of spectral lines from different atoms and molecules, we can determine the temperature of a star's photosphere quite accurately. So, for example, if we see a red star that has spectral lines due to helium, we know it must intrinsically hot and blue. Therefore, we know it must lie behind a dust cloud.
|
|
|
Optical spectra of stars of type A-F. The hottest (type O) stars have most of their radiation toward the blue side of the spectrum, while the cooler (type F) stars have more radiation at longer wavelengths. One can discriminate more accurately between spectral types by checking the ratios of spectral lines. For example, type O stars have an absorption line due to ionized helium (He+) at 4686 A, while type A stars don't. Source: Michael D'Zmura. To see the spectra of cooler stars, click here. |
For historical reasons, astronomers classify the temperatures of stars on a scale defined by
spectral types, called O B A F G K M, ranging from the hottest (type O) to the coolest (type M) stars. These spectral types are further subdivided with a decimal system, ranging from 0 (hotter) to 9.5 (cooler). Thus, the coolest type O star (T = 25,000 K*) is called O9.5, while the hottest type B star (T = 25,000 K*) is called B0. The Sun (T = 6000 K) is a type G2 star. For further details, see Perry's Stellar Atlas. You can also see how the strength of spectral lines from various elements depend on a star's spectral type by playing with this Spectral type Java Applet from the University of Oregon.
[*Experts will notice that I am being a bit loose in my definition of stellar temperatures. Because stars do not radiate exactly as blackbodies, the temperature of the gas in the photosphere is not exactly equal to the temperature defined by the color of the radiation. But this distinction is not critical for the argument here. When I quote a value of temperature here, I use "effective temperature", the temperature for which the Stefan-Boltzmann law is valid.]
Astronomers add a third Roman numeral to the spectral classification scheme to designate
luminosity class, ranging from class I (for exceptionally luminous) to V (for relatively low luminosity). Thus, for example a K0I star means a relatively cool (T = 4000) K star that is exceptionally luminous for its spectral type -- a red giant. (Sometimes astronomers add yet more letters and numbers after the luminosity class, but that is getting to a level of detail that we'll skip here.)
Since the turn of the century, with the pioneering work of
Annie Jump Cannon of Harvard College Observatory, astronomers have been classifying stars according to spectral type. We now have catalogs listing spectral types and magnitudes of several hundred thousands of stars.
(Return to course home page)
February 3, 2001
Copyright by Richard McCray
