2. STELLAR POSITIONS
Stars have three properties that are visible to the naked eye:
position, brightness, and color. These properties are extrinsic,
i.e., they depend not only on the properties of the actual star, but also on
external conditions, such as the location of the observer. To understand stars,
we must find ways to infer their intrinsic
properties from these extrinsic properties. Intrinsic properties are properties
that describe the star itself, independently of the observer, such as radius,
luminosity, surface temperature, composition, and mass.
Let's start with position: the location of a star in the sky.
Position is clearly an extrinsic property. If the Earth were located a few hundred
light years away from its present position, all the constellations would be
different. The positions of the brightest stars relative to each other would
be totally different. In fact, we can see the positions of the nearby stars
change. The motion is very slight -- the constellations look almost the same
today as they did thousands of years ago. But with very accurate measurements,
we can see the nearby stars move relative to the more distant stars by fractions
of an arcsecond (denoted ") over timescales as short as a year. These apparent
motions are the result of three actual motions: (1) the Earth's orbit around
the Sun; (2) actual motion of the nearby stars through space; and (3) the actual
motion of the Solar system through space.
|

|

|

|
|
Apparent motion of a nearby star due to the Earth's motion. The
blinking image on the right alternates the images on the left and center
of the same star field, taken six months apart. The slight annual shift
of the nearby star near the top is called parallax.
From the University
of Washington. Press the refresh button on your browser to
repeat the sequence.
|
The most important and useful kind of proper motion of nearby
stars is that due the Earth's motion around the Sun. This motion causes the
apparent positions of nearby stars to wobble back and forth annually [in circles
if the star is toward the ecliptic poles (poles of the Earth's orbit), in straight
lines if the star is in the ecliptic (equator of the Earth's orbit)]. The closer
the star, the greater the angle of wobble, called parallax.
(Precisely, parallax is half the total angle of wobble over a period of one
year.) By measuring the parallax of a star, we can infer its distance.
Actually, parallax is a phenomenon that is familiar to all of
you, although you may not have heard the name. It is illustrated in the animation
above. As you drive along the highway, the nearby trees and buildings seem to
move backwards faster than the distant mountains. In fact, the viewing angles
of the nearby objects do sweep backwards much faster than those of the distant
objects. In astronomy, the car speeding along the highway is replaced by the
Earth speeding around the Sun. Since the Earth travels around the Sun in a circle
instead of speeding along in a straight line, the angles of the nearby stars
wobble back and forth once a year. For the Earth and stars, the principle is
illustrated the animation below.
|
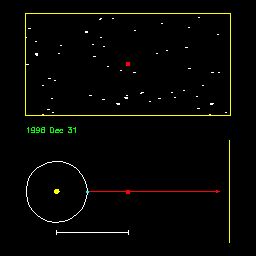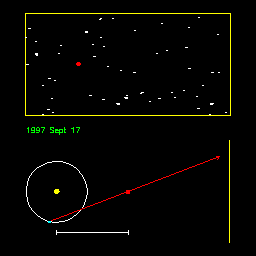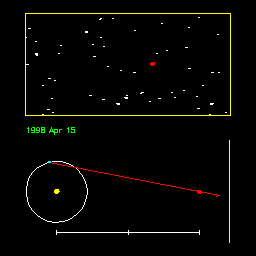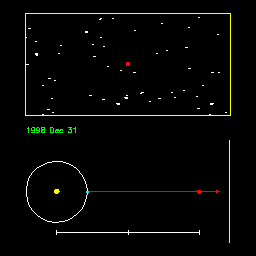
|
|
Animation illustrating the apparent motion of a nearby star (red
dot) due to the Earth's (blue dot) motion about the Sun. The apparent
motion is greater when the star is nearby (first half of animation)
and less when the star is more distant (second half). From Ohio State
University. Press the refresh button on your browser to repeat the sequence.
|
Or better yet, you can play with this Parallax
Java Applet by the University of Washington.
Parallax angles are very small because the radius of the Earth's
orbit is very small (< 10-5 times) compared to the distance to
the nearest star. In fact, the nearest bright star, a-Cen,
has a parallax of 0.753". Such an angle is no greater than the size of the blurred
stellar image seen through a telescope under conditions of very good seeing.
Astronomers can actually locate the position of a star more accurately by measuring
the average position of the center of the blur. That will give positions of
the star that are accurate to about 0.01"; but that is about the limiting accuracy
that can be achieved with ground-based telescopes.
A little trigonometry, explained here,
gives the simple formula d = 1/p,
where d stands for the
distance of the star and p
stands for the parallax angle of the star (measured in arcseconds). This formula
works if the distance is measured in units called parsecs
(pc). One parsec is equal to 3.24 light years, or 3.08 x
1016 meters. Therefore, the nearest star a
-Cen, with p = 0.753", has a distance d = 1/(0.753) = 1.33 parsecs, or (1.33
x 3.24) = 4.3 light years from the solar system.
Since astronomers can measure parallax with an accuracy of about
0.01" from the ground, they can infer the distances of stars (with decreasing
accuracy) out to about 100 pc. Here's a list of the 26
nearest stars. All are within a distance of 12 light-years.
As you will learn throughout this course, it's very important
for astronomers to be able to measure the distances to more distant stars, galaxies,
and other objects. They took a giant step in this direction with the launch
of the Hipparcos
satellite, built and operated from 1989 - 1993 by the European Space Agency.
Above the blurring effect of the Earth's atmosphere, Hipparcos measured parallaxes
with an accuracy of 0.001". With such accuracy, Hipparcos could measure the
distances of stars out to about 1000 pc (or 1 kiloparsec, 1 kpc), or about 10
times better than could be done from the ground. The Hipparcos catalog contains
some 120,000 stars.
Actually, you can think of the parallax method as a kind of
binocular vision. You have depth perception because nearby objects in the image
on the retina of your left eye are shifted a little to the right compared with
the same objects in the image on the retina of your right eye. The part of your
brain devoted to processing these images makes millions of calculations every
second to combine these shifted images of objects and your mind that they actually
come from nearby objects. You can think of two Hipparcos images of the sky taken
6 months apart as images from the left and right eyes. But in the case of the
Hipparcos images, the "left eye" and the "right eye" are separated by the diameter
of the Earth's orbit, or 2 AU.
|

|
|
The Big Dipper as seen by Hipparcos. Click here
to see this same image against a black background.
|
The image shown above is a part of the sky containing the Big
Dipper (Ursa Major) as seen by Hipparcos. It's actually a superposition of two
images, one in blue and one in red, taken 6 months apart. The red image is taken
when the Earth is to the right, so the nearby stars in the red Dipper are shifted
to the left (by about 1 cm in this picture) compared to those in the blue Dipper,
while more distant stars are shifted less. In these images the shift (or parallax
angle) is exaggerated by a large factor to make it easy to see. With red-blue
("3-d") glasses (put the red over your left eye), you can actually see the amazing
depth of this field of stars. It may take a while for the 3-d effect to come
in. Your brain must solve many thousands of equations to create this image in
your mind. You can find a few more of these fantastic images in the Hipparcos
home page. (The Hubble Space Telescope can also measure parallaxes with
comparable accuracy, but Hubble has such a narrow field of view that it would
take forever to compile a catalog with as many stars as there are in the Hipparcos
catalog.)
In addition to parallax, the positions of nearby stars move because
the stars themselves are actually moving relative to each other. These motions,
called proper motions,
and can be distinguished easily from parallax motions because they do not oscillate
with a one-year period. They appear as a steady drift in a straight line that
is combined with the oscillatory motion due to parallax to create a kind of
loopy drift. If two stars have the same transverse (sideways) velocity, the
nearer one will have a greater proper motion (i.e., will have a greater drift
angle in a given time). The star with the greatest known proper motion is called
Barnard's star. It has
a proper motion of 10.31" per year, much greater than its parallax of 0.544",
which implies that it is actually moving through space with a transverse velocity
of about 90 km/s.
Even if all the nearby stars were stationary, they would have
proper motions due to the Sun's actual motion. If the Sun were moving to the
east, the nearby stars would appear to be moving toward the west (relative to
the more distant stars). We can distinguish the apparent proper motions due
to the Sun's actual motion from those due to the stars' actual motions because
the Sun's motion will cause all the nearby stars to appear to be moving in the
same direction, whereas those motions due to the stars' actual motions will
have no such correlation.
(Return
to course home page)
Last modified October 12, 2002
Copyright by Richard McCray




