Diffraction and Angular Resolution

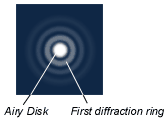
Even with a perfect lens or mirror, the sharpness of the image of a telescope (or camera or microscope) is limited by the diameter of the lens or mirror. This blurring is a consequence of the wave nature of light. Below is an image of a point-like star taken with a perfect mirror which is not very large:

The bright spot at the center is called the Airy disk, and it has an angular diameter given by the equation q = l/D, where l is the wavelength of the radiation and D is the diameter of the lens or mirror. The smaller the mirror (or the greater the wavelength), the bigger the Airy disk. On the right are three images of two stars. In the middle image the stars are separated by an angle q = l/D, and you can clearly see that there are two. But you wouldn't be able to tell that there are two stars if the angle between the stars were much smaller, or if the diameter of the telescope were smaller.

Example 1: your eye. The diameter of the pupil of your eye is about 3 millimeters and the wavelength of light is about 600 nanometers. So q = (6 x 10^-7)/(3 x 10^-3) = 2 x 10^-4 radians = 0.7 arcminutes.

Example 2: the Very Large Array of radio telescopes (VLA). The telescopes are separated by a distance of up to 36 km, so this array can obtain images as sharp as a single telescope with a 36 km diameter mirror. So, observing at a wavelength of 2 cm, the VLA will be able to resolve images down to an angular diameter q = (0.02)/(36 x 10³) = 5.6 x 10^-7 radians = 0.11 arcseconds.