SMALL ANGLES
Two systems of units are commonly used to measure angles. The most familiar is the system where a full circle is 360o, each degree is subdivided into 60 arcminutes ('), and each minute is divided into 60 arcseconds ("). Thus, there are 360 x 60 x 60 = 1,296,000" arcseconds in a full circle.
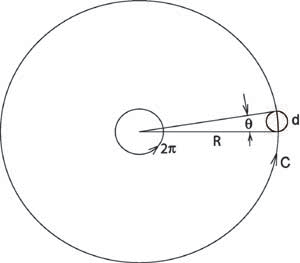
To relate angles to distances and sizes, it's more convenient to use natural angle units, called radians. A full circle is 2p radians of angle. Thus, 1 radian corresponds to 360/2p = 57.3o, or 1,296,000/2p = 206,265". To change degrees into radians, divide by 57.3o; to change arcseconds into radians, divide by 206,265.
In natural angle units, the circumference, C, of a circle is simply equal to the angle of a full circle (2p) times the radius, R: C = 2pR. Likewise, the distance along an arc, d = qR, where q is the angle in radians. If q is small, as illustrated in the figure below, then the arc length, d, is very nearly equal to the diameter of the small circle. The circle might represent a distant star or planet.

As an example, let's calculate the angular diameter of a nearby star. The nearest star has a distance from Earth of about R = 4 light years, or 4 x 1016 m and a diameter of about d = 7 x 108 m. Thus, the star subtends an angle q = d/R = (7 x 108)/(4 x 1016) = 1.75 x 10-8 radians. To change this to arcseconds, multiply by 206,265, giving q = 0.00365". This is a smaller angle than can be resolved by present-day optical telescopes. The sharpest images we have (with adaptive optics on large ground-based telescopes) have angular resolution 0.04". We need more than 10 times better angular resolution to begin to see the size of this star.