Gamow's triumph: In Section 2 of this lesson you can find a chronicle of the discovery of the cosmic fireball radiation. It is surely one of the most fascinating stories in the history of science. Be sure to review it.
As we have described, George Gamow's theory of the hot big bang was wrong. Gamow overlooked the most important reactions that determine the formation of elements in the early universe and his prediction of the temperature of the cosmic fireball radiation was off by a factor of almost 10. Yet we attribute the theory of the big bang universe to Gamow, and rightly so. He was the first scientist who dared to try to explain what the universe was like when it was only minutes old, and he realized that it must be filled with gamma rays in order to prevent nuclear reactions from turning all the matter into heavy elements. Gamow led the way by asking the right questions. After that, it was inevitable that other scientists would check his theory and correct the errors. And several did, apparently without knowing of each other's work.
George Gamow came to the University of Colorado from Washington University in 1956. He was a great popularizer of science as well as a great scientist. During the 1950s he wrote many books about astronomy, mathematics, and other branches of science intended for students at every level, from elementary to college.
Thermal history of the universe: According to the big bang theory, the universe at an age of 1 second A.B.E. is filled with radiation at a temperature of about 1010 (10 billion) K. As the universe expands, this radiation (and the matter) will cool down. By 300,000 years A.B.E., the cosmic temperature will be 3700 K, roughly the temperature of the photosphere of a red giant star.
A very important transition in the history of the universe occurs at this time, which we call the recombination epoch. Before this time, almost all the hydrogen atoms in the universe are ionized, so that the cosmic gas consists of bare protons and electrons, plus helium atoms. In such a gas, just as in the Sun's interior, a photon cannot travel far before it scatters off a free electron in the gas. The result of this diffusion is that the universe is opaque: we cannot tell where the photons were originally produced. But after the recombination epoch, the temperature is low enough that the electrons can attach to protons and remain bound to form neutral hydrogen atoms.
The photons of the cosmic background radiation, now consisting mainly of red and infrared photons, do not interact with the neutral hydrogen and helium atoms. At the recombination epoch, the universe becomes transparent. The photons that we detect in the microwave background today have traveled freely through cosmic space since the universe was only 300,000 years old. In a very real sense, the universe before the recombination epoch was like the interior of the Sun: hot and opaque. The universe after the recombination epoch is more like interstellar space: cool and transparent. Because of this analogy, we speak of the place where the radiation last interacted with matter as the cosmic photosphere.
As the universe continued to expand, the cosmic background continued to cool and the wavelengths of the photons continued to increase. According to this theory, the temperature of the cosmic background should be about 3 K at the present time.
Spectrum: In 1965, Penzias and Wilson measured a background radiation temperature of 3.5 +/- 1.0 K. At that time many scientists were not convinced that they were really seeing the radiation from the big bang. A crucial test would be to see whether the background radiation actually had the spectrum of blackbody radiation that was predicted by the theory. That test required observations of the radiation at wavelengths shorter than 2 millimeters, which could only be done from space. (The Earth's atmosphere is too bright to make such measurements from the ground.)
The issue was settled by observations with the Cosmic Background Explorer (COBE) satellite, launched in 1989. COBE observations showed that the background radiation spectrum at wavelengths less than 3 mm fit the theoretical blackbody curve to an accuracy of better than one part in 1000.
Actually, the temperature of the microwave background had already been measured in 1941 by Andrew McKellar indirectly through observations of optical absorption lines due to the cyanogen (CN) molecule in interstellar clouds. Each CN molecule acts as a tiny antenna that is tuned to absorb radiation at wavelengths of 2.64 and 1.32 mm. One can infer the intensity of this radiation by measuring the relative intensities of optical absorption lines due to these CN molecules. But in 1941 there was no theory of the big bang radiation, so few people paid any attention to the observation, and nobody recognized its significance until 25 years later.
In fact, since the late 1940s, millions of people had been observing the cosmic microwave background every day without knowing it. TV receivers are sensitive to radiation with wavelengths in the range 10 - 20 centimeters, and about 1% of the "snow" on every TV screen is due to this radiation.
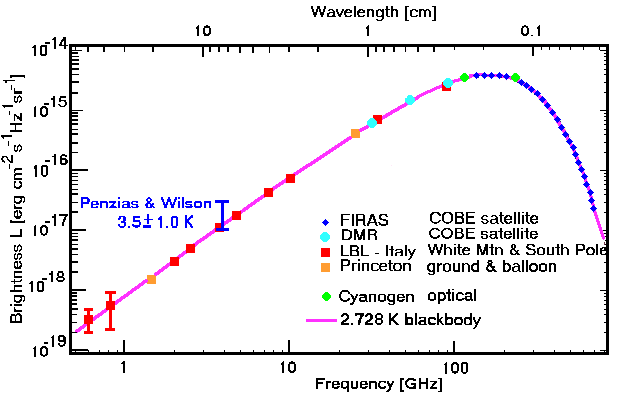
The figure below summarizes the observations of the microwave background radiation. You can see that the temperature of the background radiation, originally measured to be 3.5 +/- 1.0 K, is now known to be 2.728 K, with an accuracy better than one part in 1000.
|
|
|
Spectrum of the cosmic microwave background. The various modern observations fit exactly on the violet curve, which represents the radiation from a perfect blackbody with a temperature of 2.728 K. The blue bar represents the original 1965 measurement by Penzias and Wilson. The green dots represent the 1941 measurement by McKellar. |
Isotropy: the big bang theory not only predicts that the microwave background radiation should have a blackbody spectrum, it also predicts that the radiation should be isotropic -- i.e., that it should have the same intensity in every direction. 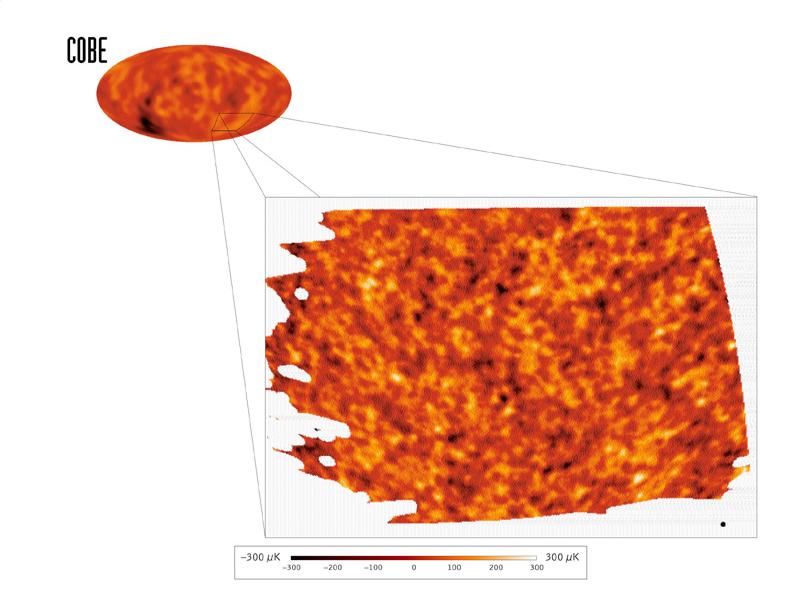We shall see that measurements of the angular distribution of the microwave background have become powerful tools for understanding the origin of structure in the universe. The figure below shows the results from COBE.
|
|
Top: light blue to red represents an increase in radiation temperature of a few parts in 1000. The radiation is slightly warmer toward the upper right because the solar system is moving in that direction with a velocity of about 600 km/s. This variation is called the "dipole asymmetry." |
|
Middle: the dipole asymmetry has been subtracted and the scale has been changed so that light blue to red now represents an increase in radiation temperature of only a few parts in 100,000. The dominant feature is the glow of dust from the Milky Way. |
|
|
Bottom: The radiation from the Milky Way has been subtracted. The residual fluctuations represent the temperature fluctuations of the "cosmic photosphere" when the universe was about 300,000 years old. |
|
|
The cosmic microwave background as observed by the COBE satellite |
|
The COBE satellite could not measure fluctuations in the microwave background with angular size less than about 7o, the diffraction limit of the telescope (see Angular Resolution). Fluctuations with smaller angular size were blurred beyond recognition. But very recently, in April 2000, a team of astronomers reported results of measurements of the microwave background made with a larger telescope carried on a balloon launched from Antarctica -- see the Boomerang home page. Their results show even stronger fluctuations on angular scales of about 1o, as illustrated below. In these new measurements, the blurring of the fluctuations is caused by the universe itself, not by the telescope.
|
|
|
The angular fluctuations of the CBR as measured by the Boomerang experiment (inset at right) compared to the fluctuations observed by COBE (upper left). The bright and dark patches in the Boomerang data differ in temperature from the average by approximately one part in 10,000. |
In the past few years, several other groups have made similar measurements of the cosmic microwave background radiation, and they have confirmed and refined the results described above. To go deeper into the physics of the cosmic microwave background radiation, see The Physics of Microwave Background Anisotropies, by Wayne Hu.
We can draw two basic conclusions from these observations:
Both of these conclusions have profound implications, as we shall now discuss.
(Return
to course home page)
Last modified April 14, 2002
Copyright by Richard McCray
