There are two main ways to estimate the age of the universe.
Cosmic expansion age: Hubble's Law says that all galaxies are moving away from each other and it follows that they were closer together at early times. In fact, one can estimate the age of the universe from Hubble's Law as follows:
Hubble's Law, V = H0D, says that the velocity, V, of a galaxy is proportional to its distance, D, from us. But the distance of a galaxy from us is its velocity times the time it has been moving: D = Vt. Putting this into Hubble's Law, we find V = H0Vt, or t = 1/H0. Taking a Hubble constant H0 = 65 km/s/Mpc, we find t = 15 billion years. If H0 is smaller, t will be larger, and conversely.
|
|
|
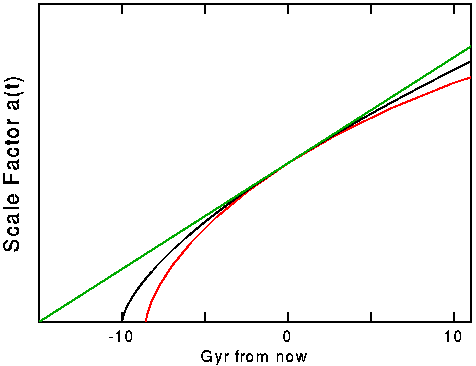
The expansion of the universe. The Hubble constant determines the slope of the curve now. In a coasting universe (green line), the expansion rate (slope) does not change, and the age of the universe is about 15 billion years. In a decelerating universe (black and red curves), the age of the universe is less. |
But this argument is oversimplified, because it is based on the assumption that the universe has always been expanding at the same rate. In fact, the universe certainly has slowed down since its early days, and it may still be slowing down. The formula D = Vt is true only if the velocity has always been constant (see above). If the velocity of a distant galaxy was once greater than it is today, the distance will be greater than implied by the above formula. In fact, for a decelerating universe with density exactly equal to the critical density (W0 = 1), the distance of a given galaxy is given by D = (3/2)Vt, in which case we find t = 2/3H0. (To see how this is derived, see The Fate of the Universe, by Team 2). This formula gives t = 10 billion years if H0 = 65 km/s/Mpc, as illustrated by the black curve above.
Globular cluster ages: Certainly, the universe can't be any older than the stars in it. As far as we know, the globular clusters are the oldest star systems in the universe; we think they were formed when the universe was less than 1/10 its present age. Therefore, the age of the universe ought to be roughly equal to the age of the globular clusters. We have already described how to determine the ages of globular clusters from the main sequence turnoff (see Lesson 5). The best estimate today is 12.6 +/- 2.2 billion years, as you can see there.
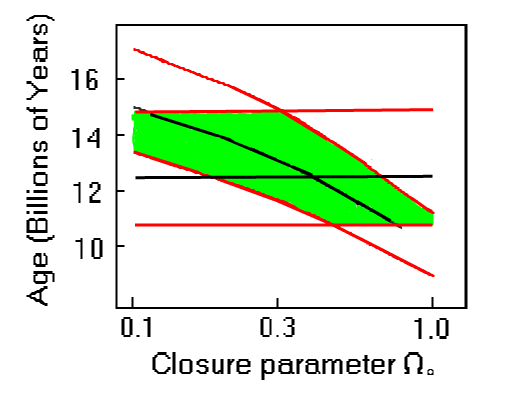
These constraints on the age of the universe are summarized in the above graph. The black horizontal line represents the best estimate of the age of the universe from globular clusters and the red horizontal lines represent the upper and lower bounds of uncertainty of the globular cluster ages. Similarly, the black curve represents the age as determined from the Hubble expansion (with H0 = 65 km/s/Mpc), while the red curves represent the upper and lower bounds of the expansion ages. These two measurements of the age of the universe are consistent if W 0 and H0 are in the green range. Thus, we can see that in a relatively low density universe (W 0 = 0.1), the permissible range of age is 13 - 15 billion years; while in a relatively high density universe (W 0 = 1), the permissible range of age is between 10.6 and 11 billion years.
