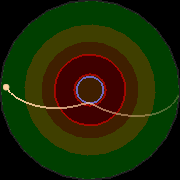
Journey into and through a Reissner-Nordström black hole
Warning:
If you fall into a black hole, you will die.
You will not go through a wormhole to another time and place.
Journey into and through the Reissner-Nordström black hole.
This one shows a map, a clock, and an artificial grid on the black hole's horizon.
A Reissner-Nordström black hole is a black hole with mass and electric charge, but no spin.
The geometry was discovered independently by
Reissner (1916)
1 and Nordström (1918)
2.
Real black holes probably spin, but probably have almost no electric charge,
because our Universe appears to be electrically neutral,
and a charged black hole would quickly neutralize
by attracting charge of the opposite sign.
Nevertheless,
the internal geometry of an electrically charged black hole
resembles mathematically that of a rotating black hole.
For this reason
the behavior inside a charged black hole
is often taken as a surrogate for that inside a rotating black hole.
The big difference between a charged (Reissner-Nordström)
and an uncharged (Schwarzschild) black hole
is that the mathematical solution to the charged black hole
has, inside its horizon, a one-way wormhole that connects to a white hole
that propels you to another space and time.
Sadly,
the wormhole is violently unstable,
and would not occur in reality.
Click on
to learn more about why the charged black hole has a wormhole.
Click on
to see what happens in reality,
and to learn more about the mass inflation instability that in reality prevents any wormhole from forming.
The background to the movie is again
Axel Mellinger's
All-Sky Milky Way Panorama (by permission).
Journey into and through the Reissner-Nordström black hole.
This one is plain.
This is the same movie as above, but without the map, clock, or grid.
Gravitationally repulsive core
Remember the
no-hair theorem
that states that an isolated black hole is characterized
(outside its horizon!) by just three quantities,
mass, charge, and spin?
Whereas the geometry for a black hole with mass and charge
— the Reissner-Norström geometry —
was discovered within a few years of Einstein's development
of general relativity,
it took until 1963 before Roy Kerr
3 discovered
the geometry of a rotating black hole.
After that, Newman et al. (1965)
4
quickly generalized Kerr's solution
to a black hole that has both charge and spin.
The no-hair theorem implies that
the Kerr-Newman geometry constitutes the most general description
of an isolated black hole outside its horizon.
As might be imagined from the long time it took
to discover black hole solutions with spin,
the Kerr-Newman geometry is technically
much more complicated
than the comparatively simple Reissner-Nordström geometry.
It is for this reason that (as of 2009)
I have yet to implement rotating black holes in the Black Hole Flight Simulator,
and instead I have used the Reissner-Nordström geometry
as a surrogate for the Kerr geometry in the visualizations on this website.
You can be sure that one day I hope to have the opportunity
to implement the Kerr-Newman geometry in the BHFS,
but it will not be easy, and it will take time.
The Reissner-Nordström (mass plus charge)
and Kerr-Newman (mass plus charge plus spin) geometries
assume that the black hole is empty
except at its singularity
(which forms a ring in the Kerr-Newman geometry).
Empty here means empty of energy-momentum —
such as that produced by matter or light —
aside from the energy-momentum of the electric field
produced by an electric charge located at the singularity.
It may come as a surprise to learn that
a Reissner-Nordström or Kerr-Newman
black hole is gravitationally repulsive in its core.
Indeed, the singularity is infinitely gravitationally repulsive.
In the case of a charged black hole,
the gravitational repulsion of the core
comes from the tension, or negative pressure,
of the radial electric field.
In relativity,
mass is a form of energy
(
E =
m c2),
so it is not surprising to learn that not only mass,
but also energy in any form,
including photons, which have energy but no rest mass, gravitate.
In a rotating black hole,
the gravitational repulsion of the core
can be explained more simply:
it's produced by the centrifugal force.
Map
|
Color
|
Zone
|
|
Green
|
Stable circular orbits
|
|
Yellow
|
Unstable circular orbits
|
|
Orange
|
No circular orbits
|
|
Red lines
|
Horizons
|
|
Red
|
Between horizons
|
Outside the outer horizon,
the orbital structure of the charged (Reissner-Nordström) black hole
is similar to that of the uncharged (Schwarzschild) black hole,
with regions where circular orbits are
stable,
unstable, and
non-existent
(compare the
Schwarzschild map).
But whereas the uncharged black hole had a single horizon,
the charged black hole has two horizons,
an outer horizon and an inner horizon.
You follow a real free-fall trajectory into and through the charged black hole.
The blue line inside the inner horizon marks the periapsis of your trajectory,
the radius of your closest approach to the center of the black hole.
Clock
The clock records the time left until you hit
the inner horizon,
which in a real black hole
is where you would be
vaporized by the
mass inflation
instability.
The time is in seconds if the black hole's mass
equals that of the supermassive black hole at the center of our Galaxy,
5 million suns.
On your trajectory,
it takes 20 seconds to fall from the outer horizon to the inner horizon.
Through the outer horizon
The trip down to outer horizon of the Reissner-Nordström black hole
is similar to that of a Schwarzschild black hole.
As you pass through the outer horizon,
the horizon splits in two,
the same as for a Schwarzschild black hole.
Without the horizon grids (right image),
there is no sign that you have crossed the horizon.
For a while, the black hole appears to increase in size
For a while, the view inside the horizon of the Reissner-Nordström black hole
continues to look similar to that inside a Schwarzschild black hole.
As you fall deeper inside the horizon, the horizon bubble enlarges.
But then the black hole appears to shrink
But as you approach the inner horizon,
the black hole ahead stops expanding,
and starts to shrink.
It looks like you are moving away from the black hole,
but that is not true.
You are still free-falling inwards, towards the black hole.
The shrinking is caused by relativistic beaming,
which concentrates the view ahead.
The same relativistic beaming
causes light from the outside universe
to become brighter and more blueshifted around the black hole.
Through the inner horizon
As you fall deeper into the black hole,
the inward flow of space is slowed
by the gravitational repulsion produced by the negative pressure of the radial electric field.
At a certain radius, the inner horizon,
the flow of space slows back down to the speed of light.
Down to this point,
it has been impossible for light or other information
to propagate upwards to you from parts of the black hole below you.
For example,
if you look at your feet,
you do see them below you,
but in fact the feet that you see
emitted their light at a time when they were
outside the current position of your eyes.
At the inner horizon,
you are hit by an infinitely bright, infinitely energetic burst of light.
The bright point of light is an image of the outside universe
reflected by the gravitationally repulsive singularity.
The burst of light contains, infinitely speeded up,
the entire history of the universe.
The infinitely bright burst of light signals the breakdown of
the Reissner-Nordström geometry.
The Reissner-Nordström geometry assumes that
all matter and charge inside the black hole
is concentrated at the central singularity.
The assumption leads to the prediction that
light from the outside universe
concentrates infinitely at the inner horizon,
which contradicts the assumption that the black hole
is empty except at its singularity.
In reality,
if there were such a thing as a charged black hole,
as you approached very close to its inner horizon,
you would see a rapidly growing explosion of light
from the outside universe.
The light triggers the
mass inflation
instability.
From the inner horizon on,
the Reissner-Nordström geometry
is not physically realistic,
despite being an exact mathematical solution to Einstein's equations.
Journey through the Reissner-Nordström black hole.
This one keeps grids all the way through.
In the standard movie,
I turned off the horizon grids just above the inner horizon
because otherwise it gets confusing.
The version of the movie at left includes horizon grids all the way through.
The horizon grids are colored with the blackbody color
that you would see if the objects emitting at the horizon
had a temperature of 4096 K
and were free-falling radially from zero velocity at infinity.
As you fall inward through the inner horizon,
a new grid appears, marking the ingoing inner horizon.
The dark red grid marking the antihorizon
becomes temporarily invisible as you turn around inside the wormhole,
but then reappears as you approach the inner horizon going outwards.
As you pass back outward through the inner horizon,
a third grid appears, the outgoing inner horizon,
or inner antihorizon.
As its
Penrose diagram
shows, the (outgoing) inner antihorizon is not the same
as the (ingoing) inner horizon.
As the white hole catapults you outward into a new universe,
a fourth grid appears, marking the white hole's outer horizon.
Through the wormhole
Inside the inner horizon,
the flow of space slows down,
turns around,
and accelerates you back out again,
back towards the radius of inner horizon.
This region inside the inner horizon is the wormhole.
The movie
at left
is an excerpt, the wormhole part,
of the longer movie linked at top of this page.
In the movie,
the camera is initially pointed inwards, towards the black hole,
but as space turns and accelerates back out,
the camera turns around and points outwards, away from the black hole.
Movie not quite what you expected?
No, it does not look much like any Hollywood depiction you may have seen.
But how could anyone draw a cameleopard before they saw what it actually looked like?
Of course, I have to surround this movie with caveats.
As I keep repeating,
in reality the wormhole would be prevented from forming by the
mass inflation
instability.
If you fell into a real black hole,
you would not go through a wormhole.
Back out through the inner horizon
The flow of space accelerates back outward.
The place where it accelerates back up to the speed of light
marks the inner horizon.
As you pass once again through the inner horizon,
this time going outward rather than inward,
you see a second infinitely bright, infinitely energetic burst of light.
Whereas on your inward passage through the inner horizon
you saw the entire history of the universe go by,
this time, on your outward passage,
you see the entire future of the universe go by.
The fact that you see the outside universe infinitely bright and blueshifted
as you pass outward through the inner horizon
was first pointed out by Roger Penrose in 1968.
Through a white hole
Accelerating past the speed of light,
the outward flow of space deposits you in a white hole,
where space is falling outward faster than the speed of light.
A white hole is like a black hole,
except time-reversed in the sense that
space in a white hole falls outward faster than light,
whereas space in a black hole falls inward faster than light.
You, inside the white hole, perceive your own proper time
to continue to move forward in the usual way.
You might have thought that,
since you originally fell through the inner horizon from a black hole,
when you passed back out through the inner horizon
you would rejoin the black hole, but this is not true.
It cannot be true,
because space cannot simultaneously fall inward and outward
faster than light.
The white hole is actually a completely separate piece of spacetime,
as is apparent in the
Penrose diagram of the Reissner-Nordström geometry.
The white hole continuation of the Reissner-Nordström geometry
is an exact mathematical solution,
but it is no more realistic than a
waterfall that falls down one side of a ravine, and then climbs smoothly up the other side.
Into a new universe
The outward flow of space in the white hole
has been propelled by the gravitational repulsion
produced by the negative radial pressure of the electric field.
As you move outward, the gravitational repulsion weakens,
and the gravitational attraction from the mass of the black hole
reasserts itself as the dominant force.
The outward flow of space decelerates.
The place where space slows back down to the speed of light
marks the outer horizon of the white hole.
As you pass outward through the outer horizon of the white hole,
for the third time you see an infinitely bright, energetic burst of light.
This time the light is from a new universe
into which you have been deposited by the white hole.
The burst of light contains the entire past history of the new universe.
As long as you were inside the white hole,
light from the new universe could not penetrate into the white hole,
since space in the white hole falls outward faster than light.
Only when you reach the outer horizon of the white hole,
where the outflow of space has slowed to the speed of light,
do you get to see light from the new universe.
The new universe is the 2MASS survey
Where is the new universe into which the white hole thrusts you?
Since the Reissner-Nordström geometry is just a mathematical solution,
it does not specify who or where or when the new universe is.
If you like, you can imagine that the new universe might be
another place and time in our own Universe.
But in reality, the Reissner-Nordström geometry is not
a physically consistent solution for a real black hole.
In reality, there is no new universe.
In the movie, the new universe is another image of our own Milky Way Galaxy,
from the
2-Micron All Sky Survey (2MASS).
Looking back at the white hole
Turning around and looking back,
you see the white hole from which you emerged.
You see light from your original Universe.
The light has traversed the same journey as you,
through the black hole, through the wormhole, through the white hole,
into a new universe.
References
-
Hans Reissner (1916)
“Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie” Annalen der Physik 355 106-120
10.1002/andp.19163550905
-
Gunnar Nordström (1918)
“On the energy of the gravitational field in Einstein's theory”
Proc. Kon. Ned. Akad. Wet. 20 1238
-
Roy P. Kerr (1963)
“Gravitational field of a spinning mass as an example of algebraically special metrics”
Phys. Rev. Lett. 11 237--238
-
E. T. (Ted) Newman, E. Couch, K. Chinnapared, A. Exton, A. Prakash, and R. Torrence (1965)
“Metric of a rotating, charged mass”
J. Math. Phys. 6 918--919